Introduction aux prismes optiques

Qu'est-ce qu'un prisme ?

Fabrication | Lumière et réfraction | Parité de l’image | Types | Guide de sélection

Les prismes sont des composants optiques en verre solide, meulés et polis pour obtenir des formes géométriques et optiquement significatives. L'angle, la position et le nombre de surfaces contribuent à définir le type et la fonction. L'une des utilisations les plus connues des prismes, démontrée par Sir Isaac Newton, consiste à disperser un faisceau de lumière blanche en ses différentes couleurs (Figure 1). Cette application est utilisée par les réfractomètres et composants spectrographiques. Depuis cette première découverte, les prismes ont été utilisés pour « courber » la lumière à l'intérieur d'un système, « plier » le système dans un espace plus petit, changer l'orientation d'une image, ainsi que pour combiner ou diviser des faisceaux optiques avec des surfaces réfléchissantes partielles. Ces utilisations sont courantes dans les applications avec les télescopes, les jumelles, le matériel d'arpentage et bien d'autres.

Figure 1 : Dispersion à travers un prisme

Une caractéristique notable des prismes est leur capacité à être modélisés comme un système de miroirs plans afin de simuler la réflexion de la lumière dans le milieu prismatique. Le remplacement des miroirs est peut-être l'application la plus utile des prismes, puisqu'ils courbent ou plient la lumière et modifient la parité de l'image. Il faut souvent plusieurs miroirs pour obtenir des résultats similaires à ceux d'un seul prisme. Par conséquent, le remplacement de plusieurs miroirs par un seul prisme permet de réduire les erreurs d'alignement potentielles, d'accroître la précision et de minimiser la taille et la complexité d'un système.

LA FABRICATION DES PRISMES

Avant d'aborder la théorie des prismes, il convient de s'intéresser à leur processus de fabrication. Pour être utilisés avec succès dans la plupart des applications, les prismes doivent être fabriqués avec des tolérances et des précisions très strictes. En raison de la variabilité de la forme, de la taille et, surtout, du nombre de surfaces, un processus automatisé à grande échelle pour la fabrication de prismes est tout à fait irréalisable. En outre, la plupart des prismes de haute précision sont généralement fabriqués en petites quantités, ce qui signifie qu'un processus automatisé ne serait pas nécessaire.

Tout d'abord, un bloc de verre (appelé « ébauche ») d'une qualité et d'un type de verre spécifiés est obtenu. Ce bloc est ensuite meulé, ou généré, par une meule diamantée en métal pour obtenir un produit presque fini. La majeure partie du verre est enlevée rapidement à ce stade, ce qui permet d'obtenir des surfaces planes, mais encore grossières (Figure 2a). À ce stade, les dimensions du futur prisme sont très proches des spécifications souhaitées. Vient ensuite un processus de meulage fin qui élimine les cassures sub-superficielles de la surface ; cette étape est connue sous le nom de rodage. Les rayures laissées par la première étape sont éliminées lors de la deuxième étape (Figure 2b). Après le rodage, les surfaces de verre doivent apparaître troubles et opaques. Au cours des deux premières étapes, la surface du prisme doit être mouillée afin d'accélérer le retrait du verre et d'éviter la surchauffe du verre lui-même.

La troisième étape consiste à polir le prisme pour obtenir la planéité de surface correctement spécifiée. À ce stade, le verre est frotté contre un polisseur en polyuréthane mouillé avec de la « boue », un composé de polissage optique généralement composé d'eau mélangée à de la pierre ponce ou de l'oxyde de cérium (Figure 2c). La durée exacte de l'étape de polissage dépend fortement des spécifications de surface requises. Une fois le polissage terminé, le chanfreinage peut commencer. Lors de cette quatrième étape, les arêtes du prisme sont soumises à une meule diamantée en rotation afin d'émousser légèrement les arêtes vives obtenues au cours des étapes précédentes (Figure 2d). Après le chanfreinage, le prisme fini est nettoyé, inspecté (par des moyens manuels et automatisés) et recouvert d'un traitement antireflets (AR) et/ou d'un miroir métallique, si nécessaire, afin d'améliorer la transmission et/ou la réflexion globale. Bien que le processus soit beaucoup plus complexe et puisse nécessiter davantage d'itérations ou d'opérations en raison du nombre de surfaces sur un prisme, les étapes de génération, de rodage, de polissage et de chanfreinage sont schématiquement décrites dans les figures 2a à 2d.

Figure 2a : Processus de fabrication des prismes : Étape de génération

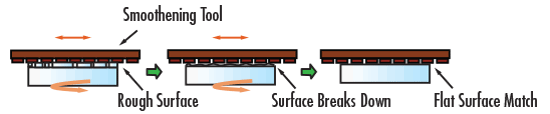
Figure 2b : Processus de fabrication des prismes : Étape de rodage

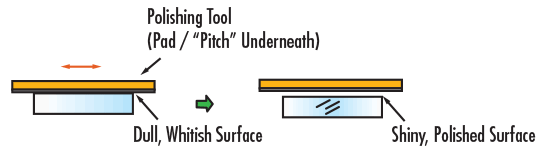
Figure 2c : Processus de fabrication des prismes : Étape de polissage

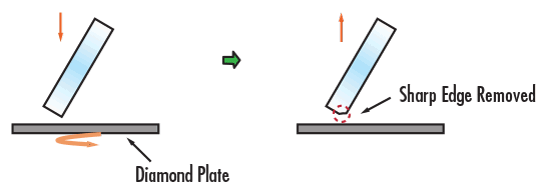
Figure 2d : Processus de fabrication des prismes : Étape de chanfreinage

Tout au long de la fabrication d'un prisme, il est nécessaire d'ajuster et de sécuriser continuellement chaque surface travaillée. Pour fixer un prisme en place, deux méthodes sont possibles : le blocage et le contactage. Le blocage consiste à disposer le prisme dans un outil métallique avec de la cire chaude. Le contactage, quant à lui, est un processus de collage optique réalisé à température ambiante, où deux surfaces de verre propres sont fixées l'une à l'autre simplement grâce à leur interaction de Van Der Waals. Le contactage est utilisé si des tolérances de haute précision sont requises car il ne nécessite pas d'ajustements supplémentaires pendant les étapes de génération, de rodage ou de polissage pour tenir compte de l'épaisseur de cire entre la surface du prisme et le bloc de contact.

À chaque étape du processus de fabrication des prismes, de la génération au blocage et au contact, un opticien qualifié doit inspecter et ajuster manuellement les surfaces des prismes sur lesquelles il travaille. Par conséquent, il s'agit d'un travail extrêmement intensif qui nécessite de l'expérience et des compétences pour être mené à bien. L'ensemble du processus nécessite souvent beaucoup de temps, de travail et de concentration.

THÉORIE : LA LUMIÈRE ET LA RÉFRACTION

Comprendre le fonctionnement d'un prisme est essentiel pour décider quel type de prisme convient le mieux à une application spécifique. Pour ce faire, il est important de comprendre comment la lumière interagit avec une surface optique. Cette interaction est décrite par la loi de la réfraction de Snell-Descartes :

Où $ \small{n_1} $ est l'indice du milieu incident, $ \small{\theta_1} $ est l'angle du rayon incident, $ \small{n_2} $ est l'indice du milieu réfracté/réfléchi, et $ \small{\theta_2} $ est l'angle du rayon réfracté/réfléchi. La loi de Snell-Descartes décrit la relation entre les angles d'incidence et de transmission lorsqu'un rayon se déplace entre plusieurs milieux (Figure 3).

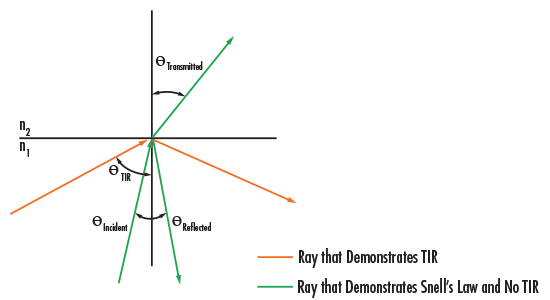
Figure 3 : Loi de Snell-Descartes et réflexion interne totale

Un prisme se distingue par sa capacité à refléter la trajectoire du rayon sans qu'il soit nécessaire d'appliquer un traitement spécial, comme c'est le cas avec un miroir. Ce résultat est obtenu grâce à un phénomène connu sous le nom de réflexion interne totale (TIR). La TIR se produit lorsque l'angle d'incidence (angle du rayon incident mesuré à partir de la normale) est supérieur à l'angle critique $ \small{\theta_c} $ :

Où $ \small{n_1} $ est l'indice de réfraction du milieu d'où part le rayon, et $ \small{n_2} $ est l'indice de réfraction du milieu d'où sort le rayon. Il est important de noter que le TIR ne se produit que lorsque la lumière se déplace d'un milieu à indice élevé vers un milieu à indice faible.

À l'angle critique, l'angle de réfraction est égal à 90°. En se référant à la Figure 3, on remarque que la TIR ne se produit que si $ \small{\theta} $ dépasse l'angle critique. Si l'angle est inférieur à l'angle critique, il y a transmission en même temps que réflexion, conformément à la loi de Snell-Descartes. Si la face d'un prisme ne répond pas aux spécifications TIR pour le(s) angle(s) souhaité(s), un traitement réfléchissant doit être utilisé. C'est pourquoi certaines applications nécessitent des versions traitées d'un prisme qui fonctionnerait bien sans traitement dans une autre application.

THÉORIE : ORIENTATION D’IMAGE/PARITÉ

Un aspect important de l'imagerie à travers un prisme est l'orientation de l'image (parité). Ce phénomène se produit chaque fois que le trajet du rayon rencontre un miroir plan, une surface réfléchissante plane ou une surface de prisme à un angle qui produit la TIR. Il existe deux types d’orientation : droite et gauche. L’orientation droite (Figure 4) décrit le cas où une image subit un nombre pair de réflexions, ce qui permet de la lire clairement (en supposant que l'image est un texte) dans au moins une position. L’orientation gauche (Figure 5) décrit le cas où l'image subit un nombre impair de réflexions, ce qui entraîne une irrégularité dans la position de l'image, comparable à ce que l'on voit dans un miroir.

Figure 4 : Image droitière ou parité paire

Figure 5 : Image gauchère ou parité impaire

Outre la parité, il existe trois types de changement d'image (Figure 6). Une inversion est un retournement d'image sur un axe horizontal, tandis qu'une inversion est un retournement d'image sur un axe vertical. Lorsque les deux opérations sont effectuées en même temps, une rotation de l'image de 180° se produit et il n'y a pas de changement de parité. Une autre façon d'envisager la parité est de la définir comme étant déterminée en regardant en arrière dans la direction de propagation vers l'objet ou l'image dans son espace optique (Figure 7).

Figure 6 : Inversion (en haut), réversion (au milieu) et rotation (en bas)

Figure 7 : Comment la parité est déterminée

Lorsque vous utilisez un prisme, tenez compte des quatre points suivants :

1. L’orientation de l'image change à chaque fois qu'une image est réfléchie.
2. Tout point du plan de la surface réfléchissante est équidistant de l'objet et de son image.
3. La loi de Snell-Descartes peut être appliquée à toutes les surfaces.
4. Lors de l'examen de l’orientation/parité de l'image, il est préférable d'utiliser une lettre non symétrique telle que R, F ou Q. Évitez d'utiliser des lettres telles que X, O, A, etc.

QU'EST-CE QUE LA TOLÉRANCE PYRAMIDALE ?

Certains prismes, comme les prismes à angle droit et les prismes en toit, ont souvent une tolérance pyramidale spécifiée ou une erreur pyramidale admissible. Il ne s'agit pas d'un des angles physiques du prisme, mais plutôt d'une manière de décrire la précision des surfaces parallèles du prisme l'une par rapport à l'autre. Si toutes les surfaces sont étendues dans un prisme parfait, la même forme se maintiendra éternellement. Il s'agirait d'une erreur pyramidale de zéro. En réalité, il y aura un léger désalignement des surfaces parallèles du prisme qui, en prolongeant les surfaces du prisme, finira par former un point pour former une pyramide. L'angle au sommet de cette pyramide théorique est l'erreur pyramidale. Elle est calculée à partir de la projection d'une arête du prisme sur la ligne située entre les arêtes de la face opposée du prisme.

Les tolérances pyramidales typiques pour les prismes de précision sont de 1 à 3 minutes d'arc. Les prismes de qualité commerciale ont souvent des tolérances de l'ordre de 5 à 10 minutes d'arc. La tolérance pyramidale est essentiellement une tolérance d'inclinaison sur les surfaces perpendiculaires aux triangles d'un prisme triangulaire. Généralement, la façon dont les prismes courbent la lumière est considérée dans un plan à deux dimensions (X-Z). L'inclinaison d'une tolérance pyramidale sera perpendiculaire à celle-ci dans le plan Y. Pour de nombreux systèmes, l'erreur pyramidale n'a que peu ou pas d'effet sur les performances et peut être corrigée en inclinant le prisme. Mais cette spécification peut être importante dans certaines applications où l'inclinaison en Y ne peut pas être inclinée mécaniquement pour compenser cette erreur. Pour ces applications, les tolérances pyramidales doivent être étroitement contrôlées. Cela peut être particulièrement problématique pour les prismes en toit.

LES TYPES DE PRISMES

Il existe quatre types principaux de prismes : prismes de dispersion, prismes de déviation, ou prismes de réflexion, prismes de rotation, et prismes de déplacement. Les prismes de déviation, de déplacement et de rotation sont courants dans les applications d'imagerie ; les prismes de dispersion sont strictement conçus pour disperser la lumière et ne conviennent donc pas à une application exigeant des images de qualité.

Prismes de dispersion

La dispersion du prisme dépend de la géométrie du prisme et de sa courbe de dispersion d'indice, basée sur la longueur d'onde et l'indice de réfraction du substrat du prisme. L'angle de déviation minimum indique le plus petit angle entre le rayon incident et les rayons transmis (Figure 8). La longueur d'onde de la lumière verte s'écarte davantage de celle du rouge, et celle du bleu davantage de celles du rouge et du vert ; le rouge est généralement défini comme étant de 656,3 nm, le vert de 587,6 nm et le bleu de 486,1 nm.

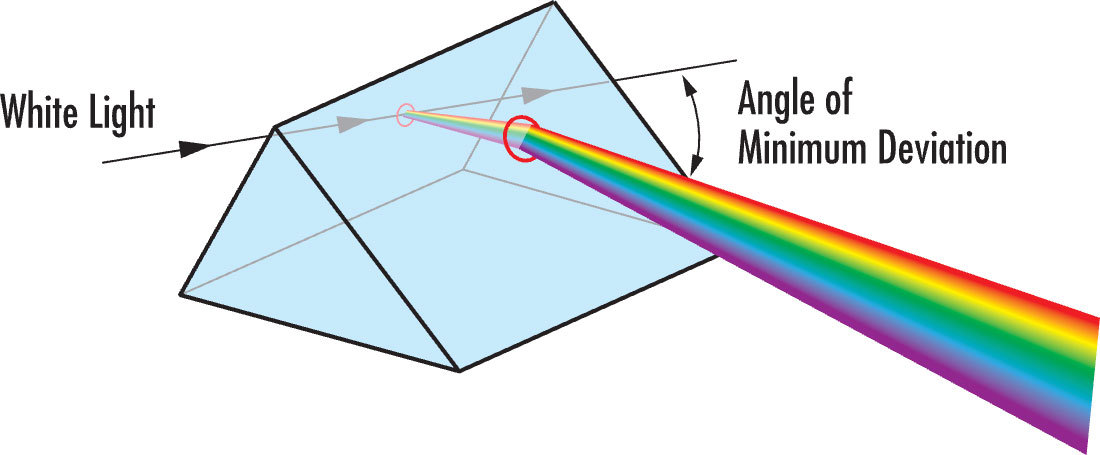
Figure 8 : La dispersion à travers un prisme

Prismes de déviation

Les prismes qui dévient la trajectoire du rayon, font pivoter l'image ou la déplacent simplement de son axe d'origine sont utiles dans de nombreux systèmes d'imagerie. Les déviations des rayons sont généralement effectuées à des angles de 45°, 60°, 90° et 180°. Cela permet de réduire la taille du système ou d'ajuster le trajet du rayon sans affecter le reste de la configuration du système.

Prismes de rotation

Les prismes de rotation, tels que les prismes Dove, sont utilisés pour faire pivoter une image après qu'elle a été inversée.

Prismes de déplacement

Les prismes de déplacement maintiennent la direction de la trajectoire du rayon, tout en ajustant sa relation avec la normale.

Guide de sélection de prismes

Pour vous aider à choisir les meilleurs prismes pour des applications spécifiques, vous trouverez ci-dessous un guide de sélection des prismes les plus couramment utilisés dans les secteurs de l'optique, de l'imagerie et de la photonique.

Guide de sélection de prismes

Prismes équilatéraux - Dispersion

Fonction Utilisés pour disperser la lumière blanche dans les couleurs de ses composantes Application Spectroscopie Télécommunications Séparation des longueurs d'onde En savoir plus

Prismes de Littrow - Dispersion, déviation

Fonction Non traité : Utilisés pour disperser la lumière blanche dans les couleurs de ses composantes Traité : Dévient la trajectoire du rayon de 60° L'image est droitière Application Spectroscopie (sans traitement) Accordage du système laser multi-spectral (traité) En savoir plus

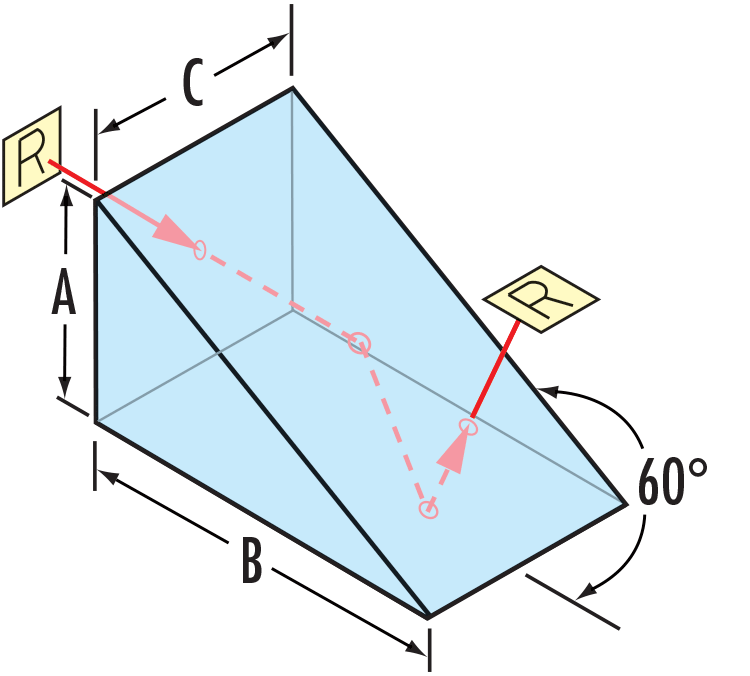
Prismes à angle droit - Déviation, déplacement

Fonction Dévient la trajectoire du rayon de 90° L'image est gauchère Utilisés en combinaison pour le déplacement d’image/de faisceau Application Endoscopie Microscopie Alignement laser Instrumentation médicale En savoir plus

Prisme penta - Déviation

Fonction Dévient la trajectoire du rayon de 90° L'image est droitière Application Ciblage visuel Projection Mesures Systèmes d'affichage En savoir plus

Prismes demi-penta - Déviation

Fonction Dévient la trajectoire du rayon de 45° L'image est droitière Application Assemblées d’érection Pechan En savoir plus

Prismes en toit Amici - Déviation

Fonction Dévient la trajectoire du rayon de 90° L'image est droitière Application Microscopes Oculaires de télescope En savoir plus

Prismes de Schmidt - Déviation

Fonction Dévient la trajectoire du rayon de 45° L'image est droitière Application Microscopes stéréo Assemblées d’érection Pechan En savoir plus

Rétroréflecteurs (prismes trièdres) - Déviation, déplacement

Fonction Dévient la trajectoire du rayon de 180° L'image est gauchère Réfléchit sur lui-même tout faisceau pénétrant dans la face du prisme, quelle que soit l'orientation du prisme. Application Interférométrie Simbleautage Télémétrie Suivi par laser Alignement de précision En savoir plus

Prismes à coin - Déviation, rotation

Fonction Utilisé individuellement pour dévier un faisceau laser d'un angle déterminé Combinez-en deux pour créer une paire anamorphique pour la mise en forme des faisceaux Application Modification de la trajectoire d’un faisceau Lasers accordables Imagerie anamorphique Sylviculture En savoir plus

Prismes rhomboïdaux - Déplacement

Fonction Déplacement de l'axe optique sans changement de main La direction reste la même (pas de déviation de rayon) Application Jumelles Télémètres Instrumentation laser En savoir plus

Prismes Dove - Rotation

Fonction Non traité : Rotation d'une image par deux fois l'angle de rotation du prisme Non traité : L'image est gauchère Traité : Réfléchissent sur eux-mêmes tout faisceau pénétrant dans la face du prisme Traité : L'image est droitière Application Interférométrie Astronomie Reconnaissance des formes Imagerie derrière les détecteurs ou dans les coins En savoir plus

Paires de prismes anamorphiques - Expansion

Fonction Extension du diamètre du faisceau incident en une seule dimension Idéaux pour rendre les faisceaux elliptiques circulaires Application Expanseurs de faisceau diode laser Objectifs d'imagerie HD En savoir plus

Lumière barres d'homogénéisation - Homogénéisation

Fonction Homogénéisent les sources de lumière non uniformes Application Éclairage LED Micro-projecteurs Réducteurs de Speckle Laser Éclairage OEM En savoir plus

Conduits lumineux/barres d'homogénéisation coniques - Homogénéisation

Fonction Homogénéiser les sources lumineuses non uniformes tout en réduisant l'ouverture numérique (NA) de sortie Application Projecteurs Systèmes de relais à micro-affichage En savoir plus

Cette introduction a donné un aperçu du processus de fabrication et de la théorie associée aux prismes, ainsi qu'une sélection pour vous aider à trouver le meilleur prisme pour votre application. Pour connaître quelques exemples d'applications du prisme, voir Exemples d'applications du prisme optique.