Aperçu du modelage de faisceaux laser

Cette note correspond aux sections 5.1, 5.2, 5.3, 5.4, 5.5 et 5.6 du Guide des Ressources en Optique Laser.

La forme d'un faisceau laser est généralement définie par sa distribution d'irradiance et sa phase. Cette dernière est essentielle pour déterminer l'uniformité du profil d'un faisceau sur sa distance de propagation. Par conséquent, les convertisseurs de faisceau sont conçus pour redistribuer l’irradiance et la phase d'un faisceau optique afin d'obtenir un profil de faisceau souhaité qui est maintenu sur la distance de propagation souhaitée. Les distributions d'irradiance les plus courantes sont les distributions gaussiennes, dans lesquelles l'irradiance diminue avec l'augmentation de la distance radiale, et les faisceaux à intensité uniforme, dans lesquels l'irradiance est constante sur une zone donnée (Figure 1). Vous trouverez une description détaillée de la propagation gaussienne du faisceau dans notre note d’application : Propagation d’un faisceau gaussien et des informations sur la quantification de la qualité de la distribution du rayonnement d'un laser dans notre note d’application : Modes de résonateurs laser.

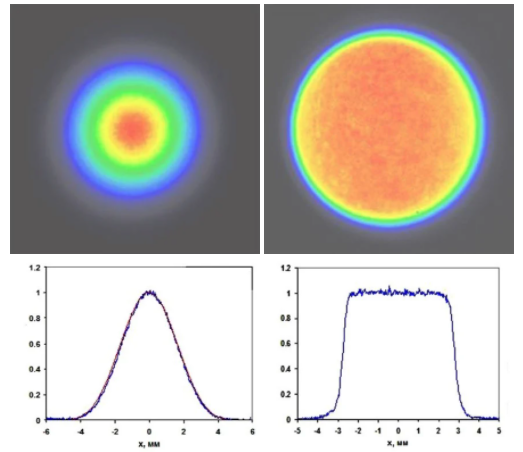
Figure 1 : Pour un profil de faisceau gaussien (à gauche), l'irradiance diminue avec l'augmentation de la distance par rapport au centre, selon une équation gaussienne. Pour un faisceau à intensité uniforme (à droite), l'irradiance est constante sur une zone donnée.

Certaines applications bénéficient de profils de faisceau différents de celui de la source laser, qui est généralement gaussien. Par exemple, les profils à intensité uniforme sont avantageux dans des applications telles que certains systèmes d’usinage de matériaux, car ils permettent souvent d'obtenir des coupes et des bords plus précis et prévisibles que les faisceaux gaussiens (Figure 2). Cependant, l'introduction d'une optique de modelage du faisceau augmente la complexité et le coût du système.

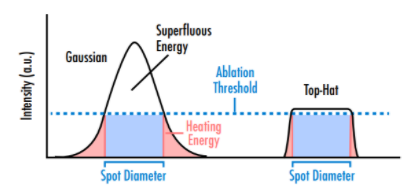
Figure 2 : Les faisceaux avec des profils gaussiens sont moins efficaces que ceux avec des profils à intensité uniforme dans les applications d'ablation laser en raison à la fois d'une grande zone de faisceau avec une énergie superflue supérieure au seuil d'ablation requis et d'une énergie inférieure au seuil dans les régions extérieures du profil gaussien.

Le modelage de faisceaux modifie les propriétés de la lumière à leur niveau le plus fondamental et son efficacité est déterminée par le principe d'incertitude d'Heisenberg sur le temps et la largeur de bande :¹

(1)$$ \Delta _x \Delta _{\nu} \geq \frac{1}{4 \pi } $$

(1)

$$ \Delta _x \Delta _{\nu} \geq \frac{1}{4 \pi } $$

x représente la position et v la quantité de mouvement. Le principe d'incertitude ajoute certaines limites à la conception des convertisseurs de faisceau. Par exemple, pour un design dont la position est très bien définie, les fréquences spatiales deviennent moins définies. En appliquant le principe d'incertitude à la théorie de la diffraction, c'est-à-dire la relation de transformation de Fourier dans l'intégrale de Fresnel, on obtient un paramètre caractéristique $ \beta $ :

(2)$$ \beta = C \frac{r_i r_o}{\lambda z} $$

(2)

$$ \beta = C \frac{r_i r_o}{\lambda z} $$

où $ \small{r_o} $ est la demi-largeur du faisceau d'entrée, $ \small{r_i} $ est la demi-largeur du faisceau de sortie, $ \small{C} $ est une constante, $ \small{\lambda} $ est la longueur d'onde, et $ \small{z} $ est la distance au plan de sortie. La valeur de $ \small{\beta} $ est très importante lors de la conception ou de l'examen d'une application de modelage de faisceau, car des valeurs plus élevées correspondent à de meilleures performances de modelage de faisceau. Par exemple, pour $ \small{\beta} < 4 $, le convertisseur de faisceau ne produira pas de résultats acceptables pour essentiellement toute application laser, tandis qu'un $ \small{ 4 < \beta <16} $ donnerait de faibles performances. Par conséquent, pour une performance optimale, il convient d'employer des conditions expérimentales qui conduisent à $ \small{\beta} > 16 $. Cette formule implique qu'il sera plus simple de concevoir des convertisseurs de faisceau pour des faisceaux plus grands, des longueurs d'onde plus courtes et des distances de mise au point plus courtes.

Modelage de faisceaux par réfraction

Dans les systèmes peu performants où le coût est un facteur déterminant, les faisceaux gaussiens peuvent être physiquement tronqués par une ouverture pour former un profil supérieur pseudo-plat. Cette méthode est inefficace et gaspille l'énergie dans les régions extérieures du profil gaussien, mais elle minimise la complexité et le coût du système.

Les applications plus performantes nécessitant une plus grande efficacité font souvent appel à des dispositifs de modelage de faisceaux laser basés sur la réfraction et diffraction. Ces ensembles utilisent généralement des éléments de phase de cartographie des champs, tels que des lentilles asphériques ou à forme libre et des éléments diffractifs, pour redistribuer l'irradiance et le profil de phase de la lumière laser. La Figure 3 montre un exemple de disposition d'un mappeur de champ réfractif qui transforme un profil de faisceau gaussien en un profil à intensité uniforme par le biais de la distorsion du front d'onde et de la condition de conservation de l'énergie.² L'amplitude et la phase du faisceau incident sont modifiées après avoir traversé les deux éléments d'un assemblage de lentilles galiléennes ou képlériennes. Le modelage du faisceau qui en résulte est très efficace (>96% de transmission) et indépendante de la longueur d'onde dans la gamme de la conception. Les convertisseurs de faisceau réfractifs permettent une distribution uniforme de l'irradiation et des fronts de phase plats.

Figure 3 : Exemple de modelage d'un faisceau réfractif à l'aide de la cartographie de champ²

Cependant, la focalisation d'un faisceau à intensité uniforme à travers une lentille n'aboutira pas à un profil à intensité uniforme au point focalisé final, car la lentille affectera le profil du faisceau. Lorsqu'un point focalisé à intensité uniforme est souhaité, les mappeurs de champ sont utilisés pour convertir les faisceaux gaussiens en profils de la tache d'Airy collimatés, qui forment des points à intensité uniforme après avoir été focalisés par une lentille sans diffraction (Figure 4).

Figure 4 : Représentation de la manière dont certains convertisseurs de faisceau, tels que le Convertisseur de Faisceau à Intensité Uniforme Focal - πShaper Q d’AdlOptica, convertissent les profils de faisceau gaussien incident en profils de la tache d’Airy de manière à obtenir des profils de faisceau à intensité uniforme après transmission à travers des optiques de focalisation.

Modelage de faisceaux par diffraction

Les dispositifs de modelage de faisceaux diffractifs utilisent la diffraction, plutôt que la réfraction, pour donner au faisceau laser une distribution d'irradiation spécifique. Les éléments diffractifs utilisent un processus de gravure pour créer une micro- ou une nanostructure spécifique dans un substrat. En général, les longueurs d'onde de conception et la fonction de l'élément dépendent respectivement de la hauteur et de l'espacement des zones. Il est donc essentiel d'utiliser un élément optique diffractif à la longueur d'onde de conception afin d'éviter les erreurs de performance. Par rapport aux dispositifs de modelage de faisceaux réfractifs, les éléments diffractifs sont également plus dépendants de l'alignement, de la divergence et de la position du faisceau dans le plan de la distance de travail nominale. D'autre part, les éléments optiques diffractifs sont très avantageux dans les configurations laser à espace limité, car ils sont généralement constitués d'un seul élément, plutôt que de multiples lentilles de réfraction.

Intégrateurs de faisceaux laser

Un intégrateur de faisceau laser, ou homogénéisateur, est composé de plusieurs microlentilles, qui divisent le faisceau en un ensemble de faisceaux plus petits, suivis d'une lentille ou d'un autre élément de focalisation qui superpose les petits faisceaux au plan cible. Ils peuvent être utilisés avec la lumière laser cohérente et d'autres sources de lumière incohérente. En général, le profil final du faisceau de sortie est la somme des motifs de diffraction déterminés par le réseau de microlentilles. La plupart des intégrateurs de faisceaux laser sont utilisés pour générer un profil à intensité uniforme à partir de faisceaux gaussiens incidents. Les homogénéisateurs de faisceau souffrent généralement de fluctuations aléatoires de l'irradiation, ce qui entraîne un profil de faisceau qui n'est pas parfaitement plat. Les intégrateurs de faisceau non basés sur la diffraction, tels que les intégrateurs d'imagerie ou les guides d'ondes, conviennent également à la lumière incohérente dans l'espace. Le choix entre les intégrateurs de faisceau de diffraction ou d'imagerie dépend du nombre de Fresnel. En règle générale, pour des nombres de Fresnel <10, un intégrateur d'image sera nécessaire pour obtenir un profil à intensité très uniforme.³

	Réfractif	Diffractif	Intégrateurs de faisceaux
Le principe du modelage	Déterministe	Déterministe	Aléatoire ou quasi-aléatoire
Fluctuations aléatoires	Faible	Faible	Élevée
Sensibilité à l'alignement	Faible	Faible	Élevée
Uniformité du faisceau de sortie	Élevée	Moyenne-élevée	Faible
Coût	Élevé	Moyen	Faible
Empreinte	Grande	Petite	Petite

Tableau 1 : Ce tableau compare les différentes technologies de modelage des faisceaux laser.

Axicons pour générer des faisceaux de Bessel

Jusqu'à présent, nous avons abordé le modelage de la lumière à l'aide de la cartographie de champ ou de l'intégration de faisceaux, où les effets de diffraction jouent un rôle majeur dans la conception et les performances de l'optique. La diffraction est la déviation de la lumière qui ne se propage pas en ligne droite et qui n'est pas causée par la réflexion ou la réfraction. Ces effets de diffraction font diverger les faisceaux laser lorsqu'ils se propagent. En revanche, un faisceau dont le profil est décrit par une fonction de Bessel, qui est définie comme la solution exacte et invariante de l'équation de Helmholtz, ne subit pas de diffraction, c'est-à-dire qu'il ne s'étale pas au cours de sa propagation.⁴ Ces faisceaux sont également autoréparables, ce qui signifie qu'ils peuvent se reformer en tout point après une obstruction. Cependant, les faisceaux de Bessel idéaux sont impossibles à générer car ils nécessiteraient une quantité infinie d'énergie. En revanche, des faisceaux de Bessel approximatifs, appelés faisceaux quasi-Bessel, peuvent être générés par l'interférence d'ondes planes formées par une surface conique telle qu'un axicon.

Les axicons forment un faisceau quasi-Bessel avec une diffraction quasi nulle sur une région donnée, appelée profondeur de champ (DOF). Après cette région, le faisceau continue à se propager en forme d'anneau (Figure 5). Les axicons réfractifs traditionnels sont considérés comme des lentilles coniques ou des prismes. La lumière les traverse et se réfracte ensuite sur la surface conique. Des axicons réflectifs avec une surface conique réfléchissante sont également employés dans certaines situations telles que les systèmes laser à impulsions ultracourtes. La large bande de longueurs d'ondes inhérente aux laser à impulsions ultracourtes connaîtrait une dispersion chromatique importante lors de la transmission à travers un axicon réfractif, alors que cette dispersion est évitée dans les axicons réfléchissants (Figure 6). Les faisceaux quasi-Bessel peuvent également être générés par des méthodes holographiques avec des rendements de diffraction élevés, mais souffrent d'un profil axial modulé par la diffraction.

Figure 5 : Schéma d’un axicon réfractif traditionnel montrant la région du faisceau de Bessel dans la profondeur de champ et le faisceau en forme d’anneau qui se propage après la région de chevauchement.

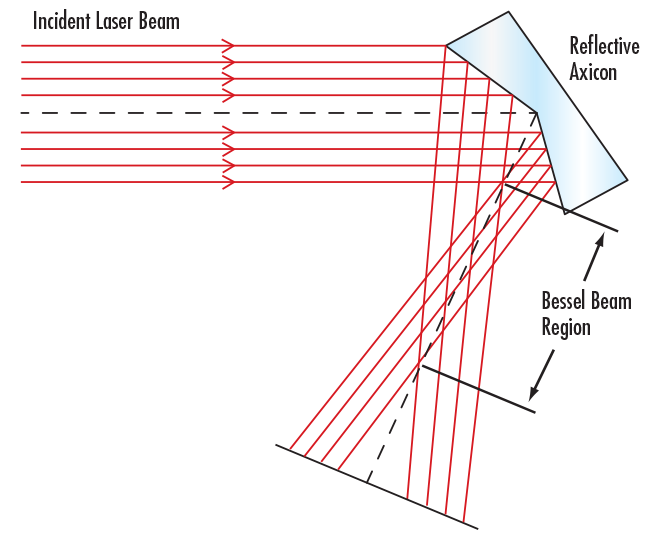
Figure 6 : Schéma d'un axicon réfléctif qui, comme l'axicon traditionnel, crée une région de faisceau de Bessel dans la profondeur de champ et un faisceau en forme d'anneau après la région de chevauchement mais, contrairement aux axicons traditionnels, est indépendant de la longueur d'onde.

Les faisceaux de Bessel subissent peu ou pas de diffraction sur leur distance de propagation et offrent une excellente DOF, ce qui les rend idéaux pour des applications telles que le traitement des matériaux par laser et la chirurgie cornéenne. Des coupes nettes avec des bords tranchants peuvent être générées dans la DOF en raison du diamètre uniforme du faisceau.

Circularisation de faisceaux avec des lentilles cylindriques

Un autre type de modelage du faisceau laser est la circularisation d'un faisceau, qui consiste à convertir un profil ovale ou de forme différente en un profil circulaire. Les diodes laser sans optique de collimation auront des angles de divergence différents dans les axes x et y en raison de la forme rectangulaire de la région active de la diode, ce qui donne des formes de faisceau oblongues (Figure 7). Les profils circulaires sont souvent souhaités pour former des points finaux symétriques, compacts et focalisés.

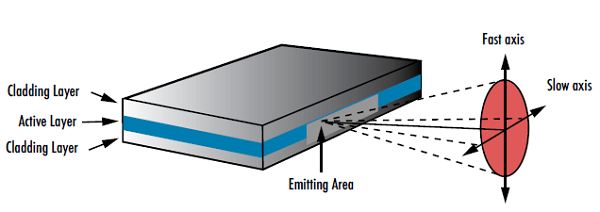
Figure 7 : La géométrie des diodes laser entraîne des faisceaux elliptiques présentant deux angles de divergence différents

Comme les lentilles sphériques standard, les lentilles cylindriques utilisent des surfaces courbes pour faire converger ou diverger la lumière, mais elles n'ont un pouvoir optique que dans une seule dimension. Les lentilles cylindriques n'affectent pas la lumière dans la dimension perpendiculaire. Cela ne peut pas être réalisé en utilisant des lentilles sphériques standard, car la lumière se concentre ou diverge uniformément de manière symétrique en rotation. Cette propriété des lentilles cylindriques les rend utiles pour former des nappes de lumière laser et circulariser des faisceaux elliptiques.

Le système de référence des lentilles cylindriques est défini par deux dimensions orthogonales : la direction de puissance et la direction de non-puissance. La « direction de puissance » s'étend le long de la longueur incurvée de la lentille et constitue le seul axe de la lentille ayant une puissance optique (Figure 8). La « direction de non-puissance » de la lentille cylindrique s'étend sur la longueur de la lentille sans aucune puissance optique. La longueur de la lentille cylindrique dans le sens de la non-puissance peut varier sans affecter la puissance optique de la lentille. Les lentilles cylindriques peuvent avoir une variété de facteurs de forme, notamment des formes rectangulaires, carrées, circulaires et elliptiques.

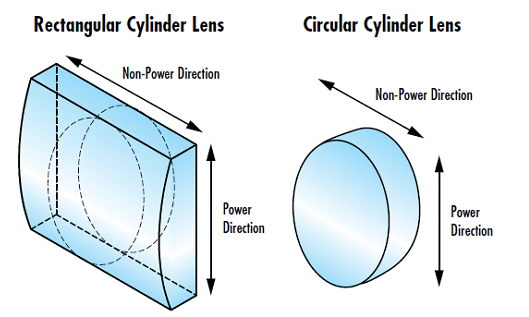
Figure 8 : Directions de puissance et de non-puissance dans les lentilles cylindriques rectangulaires et circulaires

Comme les diodes laser divergent de manière asymétrique, une optique sphérique ne peut pas être utilisée pour produire un faisceau collimaté circulaire à partir d'une diode. La lentille agit sur les deux axes en même temps, ce qui maintient l'asymétrie originale du faisceau. Chaque axe peut être traité séparément en utilisant une paire orthogonale de lentilles cylindriques.

Le rapport des distances focales des deux lentilles doit correspondre au rapport des divergences x et y du faisceau afin d'obtenir un faisceau de sortie symétrique. Comme pour la collimation standard, la diode laser est placée au point focal commun des deux lentilles et la distance entre les lentilles est maintenue égale à la différence de leurs distances focales (Figure 9).

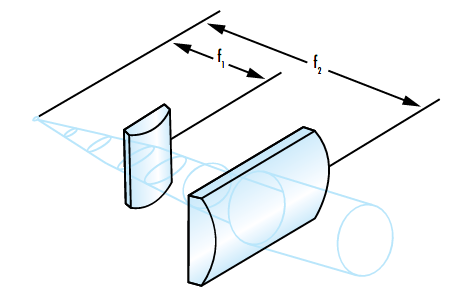
Figure 9 : Exemple de circularisation d'un faisceau elliptique à l'aide de lentilles cylindriques.

Les petites ouvertures de sortie des diodes laser peuvent conduire à des angles de divergence très importants, ce qui peut poser problème lorsqu'on essaie de collimater le faisceau. La divergence a un effet direct à la fois sur la longueur admissible du système et sur les dimensions requises des lentilles. La relation entre la divergence et la taille du faisceau est décrite dans notre note d’application Propagation d’un faisceau gaussien. Les positions relatives de chaque lentille cylindrique étant relativement fixes en fonction de leur distance focale, il est possible de calculer la largeur maximale du faisceau $ \left( \small{d} \right) $ au niveau de chaque lentille en utilisant la distance focale de la lentille $ \left( \small{f} \right) $ et l'angle de divergence $ \left( \small{\theta} \right) $ de l'axe que la lentille collimate. L’ouverture utile de chaque lentille doit alors être plus grand que la largeur maximale du faisceau correspondante pour éviter de tailler le faisceau.

(3)$$ d = 2 f \times \tan{\left( \frac{\theta}{2} \right)} $$

(3)

$$ d = 2 f \times \tan{\left( \frac{\theta}{2} \right)} $$$

Pour en savoir plus, consultez notre note d’application : Considérations relatives à l’utilisation de lentilles cylindriques.

Circularisation de faisceaux avec des paires de prismes anamorphiques

Les paires de prismes anamorphiques sont d'autres types d'optiques utilisées pour circulariser les faisceaux elliptiques. Les paires de prismes anamorphiques consistent en deux prismes utilisés ensemble pour remodeler un faisceau laser. Ils sont généralement utilisés pour transformer des profils de faisceau elliptiques en distributions circulaires, mais ils peuvent également produire d'autres profils de faisceau elliptiques dans une variété de tailles. Le principe optique en jeu derrière le remodelage est le même que celui des lentilles cylindriques : la réfraction. La lumière est courbée dans une direction, ou un axe, tandis que l'autre axe reste constant (Figure 10). Cela permet de compenser les différents angles de divergence du faisceau.

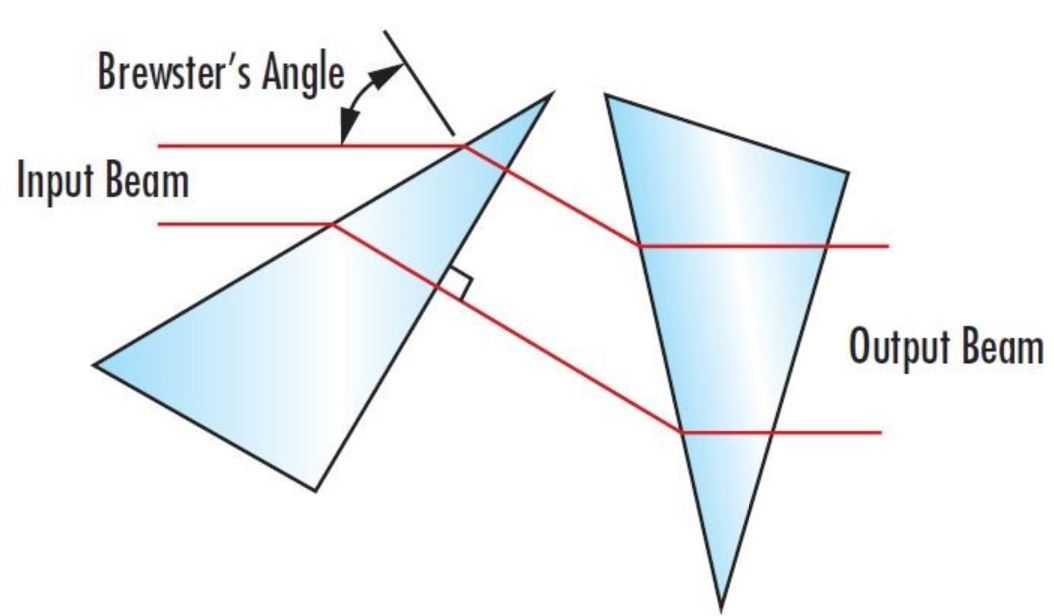
Figure 10 : Une paire de prismes anamorphiques agissant comme un expanseur de faisceau dans une direction, qui peut circulariser un faisceau elliptique.

Un seul prisme peut changer le rayon du faisceau dans un seul axe, mais cela peut également changer la direction du faisceau. Deux prismes sont nécessaires pour maintenir la direction originale de propagation du faisceau tout en manipulant son ellipticité. Les paires de prismes anamorphiques maintiennent le parallélisme avec la direction d'origine, mais elles déplacent le faisceau dans la direction perpendiculaire. L'utilisation de paires de prismes anamorphiques nécessite également un alignement angulaire précis pour un bon fonctionnement. Bien que cela ne soit pas nécessaire, il est utile qu'un prisme soit orienté à l'angle de Brewster, qui est l'angle d'incidence auquel il n'y a pas de réflexion de la lumière à polarisation p. L'autre surface du prisme serait à incidence normale par rapport au faisceau et doit être traitée antireflets (AR) pour maximiser la transmission. L'alignement précis requis conduit de nombreux intégrateurs de systèmes optiques à les acheter sous forme de paire pré-alignée.

Les diodes laser haut de gamme ont souvent des paires de prismes anamorphiques intégrées dans la tête du laser pour la circularisation du faisceau. De nombreuses diodes moins coûteuses n'en ont cependant pas. Le coût d'achat d'une paire de prismes anamorphiques séparée et d'une diode moins chère ne comportant pas de paire de prismes anamorphiques intégrée peut être inférieur à celui d'une diode plus chère.

Les lentilles cylindriques ont plus de degrés de liberté que les paires de prismes anamorphiques montés, ce qui les rend plus difficiles à aligner. Les lentilles cylindriques peuvent s'incliner, ce qui rend les prismes anamorphiques plus indulgents lorsqu'on tente d'aligner les axes indépendamment. Il faut également porter une attention particulière à la distance focale des lentilles cylindriques afin qu'elles soient placées à la bonne distance de la sortie de la diode laser pour produire un faisceau de sortie collimaté et circularisé. Les paires de prismes anamorphiques montées sont plus faciles à utiliser. Elles sont pré-alignées pour un pouvoir d'expansion fixe, ce qui élimine le besoin de les positionner et de les assembler vous-même comme vous le feriez avoir avec des lentilles cylindriques. Les prismes n'ont qu'un seul axe qui doit être aligné indépendamment, car l'utilisateur ne fait que glisser le prisme dans la trajectoire du faisceau. Cela supprime une étape d'alignement, ce qui permet à l'utilisateur de gagner du temps et d'éviter des frustrations potentielles. L'emplacement physique des prismes anamorphiques, par rapport à l'emplacement du faisceau laser incident, est également moins sensible.

Toutefois, les degrés de liberté supplémentaires offerts par des lentilles cylindriques leur confèrent une plus grande flexibilité, ce qui peut être utile pour les applications de recherche et le prototypage. Les lentilles cylindriques peuvent également offrir un débit plus élevé que les paires de prismes anamorphiques, en particulier lorsque les lentilles comportent des traitements AR. La lumière traverse moins de matière dans les lentilles cylindriques que dans les paires de prismes anamorphiques, et la lumière à polarisation p sera perdue si les prismes anamorphiques sont utilisés à l'angle de Brewster. Pour plus d'informations, veuillez consulter notre note d'application : Paires de prismes anamorphiques.

	Lentilles Cylindriques	Paires de Prismes Anamorphiques
Déplacement du faisceau	Pas de déplacement	Déplacement
Degrés de liberté	Élevés	Faibles
Sensibilité à l'alignement	Élevée	Faible
Rendement	Élevé	Moyen
Coût	Faible	Faible
Empreinte	Petite	Petite

Tableau 2 : Comparaison des lentilles cylindriques aux paires de prismes anamorphiques pour la circularisation du faisceau.

Références

F. M. Dickey and S. C. Holswade, Laser Beam Shaping: Theory and Techniques, Marcel Dekker, New York (2000).
Laskin, Alexander, and Vadim Laskin. "Refractive field mapping beam shaping optics: important features for a right choice." Proc. ICALEO. Vol. 2010. (2010).
F.M. Dickey, S.C. Hoswade, D.L. Shealy, Laser Beam Shaping Applications, Taylor & Francis, ISBN 0-8247-5941 (2005).
J. Durnin : J. Opt. Soc. Am. A 4 (1987) 651.

Section précédente Section suivante

Plus de ressources

Ce contenu vous a-t-il été utile ?

Merci d'avoir évalué ce contenu !