Comprendre les spécifications optiques
Caractéristiques de Fabrication | Caractéristiques de la Surface | Caractéristiques des Matériaux
Les caractéristiques optiques sont utilisées tout au long de la conception et la fabrication d'un composant ou d'un système, pour déterminer de quelle façon il répond à certaines exigences de performance. Ces caractéristiques sont utiles pour deux raisons : d'abord, elles précisent les limites acceptables des paramètres clés qui régissent la performance du système, ensuite elles précisent la quantité de ressources (c.-à-d. le temps et le coût) qui devrait être consacrée à la fabrication.
Un système optique peut subir une sous-spécification ou une sur-spécification qui peuvent toutes deux entraîner des dépenses en ressources inutiles. La sous-spécification se produit lorsque les paramètres nécessaires ne sont pas tous correctement définis, ce qui entraîne une performance insuffisante. La sur-spécification se produit lorsqu'un système est défini de manière trop serrée, sans tenir compte de l'évolution des besoins optiques ou mécaniques, ce qui entraîne un coût plus élevé et une difficulté de fabrication accrue.
Pour mieux comprendre les caractéristiques optiques, il est important d'examiner tout d'abord ce qu'elles signifient. Pour simplifier leur nombre sans cesse croissant, regardons plus précisemment la fabrication de base des composants, leur surface, et les caractéristiques liées aux matériaux des éléments optiques tels que des lentilles, miroirs, fenêtres, filtres, polariseurs, prismes, séparateurs, réseaux, ou encore fibres optiques. Ainsi identifier leur fabrication de base permet d'obtenir des informations premières essentielles pour comprendre pratiquement tout produit optique.
CARACTÉRISTIQUES DE FABRICATION
Tolérance du Diamètre
La tolérance de diamètre d'un composant optique circulaire fournit la gamme de valeurs acceptable pour le diamètre. Cette caractéristique de fabrication peut varier en fonction de la compétence et des capacités du fabricant optique. Bien que la tolérance de diamètre n'ait aucun impact sur la performance optique de l'optique elle-même, il s'agit d'une tolérance mécanique très importante qui doit être envisagée si l'optique doit être montée sur n'importe quel type de support. Par exemple, si le diamètre d'une lentille dévie de sa valeur nominale, il est possible que l'axe mécanique puisse être déplacé de l'axe optique dans un ensemble monté, provoquant ainsi son décentrage (Figure 1). Les tolérances de fabrication type du diamètre sont les suivantes : +0,00/-0,10 mm pour une qualité type, +0,00/-0,050 mm pour une qualité de précision, et +0,000/-0,010 mm pour une qualité élevée.

Figure 1: Décentrage d'un Faisceau Collimaté
Tolérance de l'Épaisseur Centrale
L'épaisseur au centre d'un composant optique, notamment une lentille, est l'épaisseur du matériau du composant mesuré au centre. Cette épqisseur est mesurée sur l'axe mécanique de la lentille, défini comme l'axe situé exactement au milieu des bords extérieurs. La variation de l'épaisseur au centre d'une lentille peut affecter la performance optique car l'épaisseur centrale mais aussi le rayon de courbure, déterminent la longueur du chemin optique des rayons qui traversent la lentille. Les tolérances de fabrication type de l'épaisseur centrale sont les
suivantes : ± 0,20 mm pour une qualité type, ± 0,050 mm pour une qualité de précision, et ± 0,010 mm pour une qualité élevée.
Rayon de courbure
Le rayon de courbure est défini comme étant la distance entre le vertex d'un composant optique et le centre de courbure. Il peut être positif, nul ou négatif, selon que la surface est convexe, plane ou concave. Le fait de connaître la valeur du rayon de courbure permet de déterminer la longueur du chemin optique des rayons traversant la lentille ou le miroir, et joue également un rôle pour déterminer le pouvoir réfringent de la surface. Les tolérances types de fabrication du rayon de courbure sont généralement ± 0,5 %, mais peuvent également être aussi basses que ± 0,1 % dans les applications de précision ou de ± 0,01 % pour les besoins de très haute qualité.
Centrage
Le centrage, également connu sous le nom de centration ou décentrement, d'une lentille est spécifié en termes de déviation du faisceau δ (1e équation). Une fois la déviation du faisceau connue, l'angle de coin W peut être calculé par une relation simple (2e équation). La quantité de décentrement dans une lentille, est le déplacement physique de l'axe mécanique par rapport à l'axe optique. L'axe mécanique d'une lentille est simplement l'axe géométrique de la lentille et est défini par son cylindre extérieur. L'axe optique d'une lentille est défini par les surfaces optiques et représente la ligne qui relie les centres de courbure des surfaces. Pour tester le centrage, une lentille est placée dans une coupelle sur laquelle une pression est exercée. La pression appliquée à la lentille situe automatiquement le centre de courbure de la première surface au centre de la coupelle, qui est également aligné avec l'axe de rotation (Figure 2). La lumière collimatée dirigée le long de cet axe de rotation, est envoyée à travers la lentille et converge au plan focal arrière. Étant donné que la lentille tourne lorsqu'on fait tourner la coupelle, tout décentrement de la lentille provoquera la divergence du faisceau orienté et tracera un cercle de rayon Δ au niveau du plan focal arrière (Figure 1).
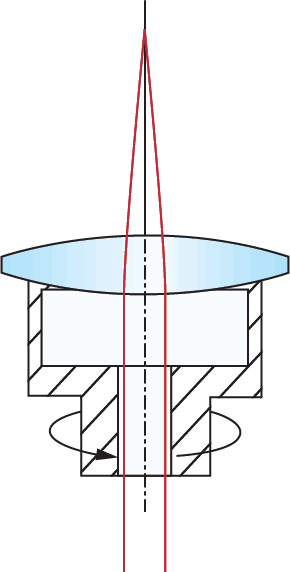
Figure 2: Test de Centrage
où W est l'angle de coin, souvent indiqué en minutes d'arc, et n est l'indice de réfraction.
Parallélisme
Le parallélisme décrit de quelle manière deux surfaces sont parallèles l'une par rapport à l'autre. Il est utile pour spécifier des composants tels que des fenêtres et des polariseurs, lorsque les surfaces parallèles sont idéales pour la performance du système, car elles réduisent la distorsion susceptible sinon de dégrader l'image ou la qualité du faisceau. Les tolérances types vont de 5 minutes d'arc à quelques secondes d'arc.
Tolérance d'Angle
Avec des composants tels que des prismes et des séparateurs, les angles entre les surfaces sont essentiels pour la performance de l'optique. Cette tolérance d'angle est généralement mesurée à l'aide autocollimateur, dont la source émet de la lumière collimatée. L'autocollimateur tourne autour de la surface de l'optique jusqu'à ce que la réflexion retour de Fresnel produise un spot lumineux sur le dessus de la surface en cours d'inspection. Cela permet de vérifier que le faisceau collimaté rencontre la surface à une incidence tout à fait normale. L'autocollimateur est ensuite tourné autour de l'optique afin que la surface optique suivante suive la même procédure. La Figure 3 montre une configuration d'autocollimateur type mesurant la tolérance d'angle. La différence d'angle entre les deux positions mesurées, est utilisée pour calculer la tolérance entre les deux surfaces optiques. La tolérance d'angle peut être considérée comme une tolérance de quelques minutes d'arc à quelques secondes d'arc.
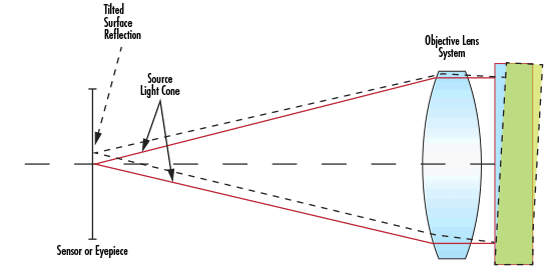
Figure 3: Autocollimateur Mesurant la Tolérance d'Angle
Biseau
Les angles en verre peuvent être très fragiles, il est donc important de les protéger lors de la manipulation ou lors du montage du composant. Ainsi, la façon la plus habituelle de protéger ces coins est d'en biseauter les bords. Les biseaux servent de chanfreins de protection et empêchent les éclats aux rebords. Ils sont définis par la largeur de leur côté et leur angle (Figure 4).

Figure 4: Biseau sur une Lentille Optique
Les biseaux sont le plus souvent coupés à 45° et la largeur de leur côté est déterminée par le diamètre de l'optique. Les optiques ayant des diamètres inférieurs à 3,00 mm, comme les micro-lentilles ou les micro-prismes, ne sont généralement pas biseautés en raison de l'improbabilité de créer des éclats aux rebords durant le processus. Il est important de noter que pour de petits rayons de courbure, par exemple, les lentilles dont le diamètre est supérieur à 0,85 fois le rayon de courbure, aucun biseau n'est requis en raison du grand angle entre la surface et le bord de la lentille. Pour tous les autres diamètres, les largeurs maximales du côté sont reportées dans le Tableau 1.
| Tableau 1 : Tolérances du Biseau | |
|---|---|
| Diamètre | Largeur Maximale du Côté du Biseau |
| 3.00mm – 5.00mm | 0.1mm |
| 5.01mm – 25.4mm | 0.25mm |
| 25.41mm – 50.00mm | 0.3mm |
| 50.01mm – 75.00mm | 0.4mm |
Ouverture Utile
L'ouverture utile est définie comme le diamètre ou la taille d'un composant optique à l'intérieur de laquelle le composant doit répondre aux spécifications. En dehors de celle-ci, les fabricants ne garantissent pas que l'optique respectera les spécifications indiquées. En raison de contraintes de fabrication, il est pratiquement impossible de produire une ouverture utile exactement égale au diamètre, ou au périmètre d'une optique. Des ouvertures utiles types de lentilles sont indiquées dans le Tableau 2.

Figure 5: Graphique Indiquant l'Ouverture Utile et le Diamètre d'un Filtre
| Tableau 2 : Tolérances de l'Ouverture Utile | |
|---|---|
| Diamètre | Clear Aperture |
| 3.00mm – 10.00mm | 90% de Diamètre |
| 10.01mm - 50.00mm | Diamètre – 1mm |
| ≥ 50.01mm | Diamètre – 1.5mm |
CARACTÉRISTIQUES DE LA SURFACE
Qualité de Surface
La qualité de surface d'une surface optique décrit son aspect esthétique et comprend comme défauts des rayures, des pics ou des creux, le plus souvent connu sous le nom de scratches and digs. Dans la plupart des cas, ces défauts de surface sont purement esthétiques et ne modifient pas grandement la performance du système. Cependant, ils peuvent causer une petite perte de transmission dans le système et une légère augmentation de la lumière dispersée. Certaines surfaces sont toutefois plus sensibles à ces effets, comme : (1) les surfaces au plan image, parce que ces défauts sont situés au point de focalisation et (2) les surfaces qui recoivent des niveaux de puissance élevés parce que ces défauts peuvent entraîner une absorption accrue de l'énergie et endommager l'optique. La spécification la plus courante utilisée pour la qualité de surface est la caractéristique de scratches and digs décrite par la norme MIL-S-13830A. La désignation de rayure est déterminée en comparant les rayures d'une surface à une série de rayures standard, dans des conditions d'éclairage contrôlées. Ainsi, la désignation de rayure ne décrit pas la véritable rayure par elle-même, mais la compare plutôt à une rayure standardisée selon la norme MIL-Spec. La désignation de creux cependant, se rapporte directement au creux, ou petit trou de la surface. La désignation de creux est calculée par le diamètre du creux en microns, divisé par 10. Les caractéristiques de scratches and digs de 80-50 sont généralement considérées comme étant de qualité standard, celles de 60-40 comme une qualité de précision et celles de 20-10 comme une qualité de haute précision.
Planéité de Surface Plane (Flatness)
La planéité de surface plane (flatness) est une caractéristique de précision de surface qui mesure l'écart d'une surface plane comme celle d'un miroir, d´une fenêtre, d´un prisme, ou d´une lentille plane. Cet écart peut être mesuré à l'aide d'une optique plane, qui est une surface de référence plane de haute qualité et de haute précision, utilisée pour comparer la planéité d'un échantillon. Lorsque la surface plane de l'optique sous test est placée contre l'optique plane, des franges apparaissent et leur forme détermine la planéité de la surface de l'optique en cours d'inspection. Si les franges sont régulièrement espacées, droites et parallèles, alors la surface de l'optique en cours d'inspection propose une même planéité que l'optique plane de référence. Si les franges sont incurvées, leur nombre entre deux lignes imaginaires, l'une tangente au centre d'une frange et l'autre aux extrémités de cette même frange, indiquera l'erreur de planéité. Les écarts de planéité sont souvent mesurés en valeurs d'onde (λ), qui sont des multiples de la longueur d'onde de la source de test. Une frange correspond à 1/2 d'une longueur d'onde. La planéité 1λ est considérée être un indice type, la planéité λ/4 un indice de précision et la planéité λ/20 un indice de haute précision.
h3>Planéité de Surface Incurvée (Power)
L'erreur sphérique est une spécification pour la précision de surfaces courbées ou avec une puissance optique. Elle est testée d'une manière similaire à la planéité, en ce sens qu'une surface courbe est comparée à une surface de référence avec un rayon de courbure hautement calibré. En utilisant le même principe d'interférence causé par les espaces d'air entre les deux surfaces, le motif de franges de l'interférence est utilisé pour décrire la déviation de la surface testée par rapport à la surface de référence (Figure 6). Une déviation de la pièce de référence créera une série d'anneaux, connus sous le nom d'Anneaux de Newton. Plus il y a d'anneaux, plus la déviation est importante. Le nombre d'anneaux sombres ou lumineux, et non pas la somme des deux, correspond au double du nombre d'ondes d'erreur.
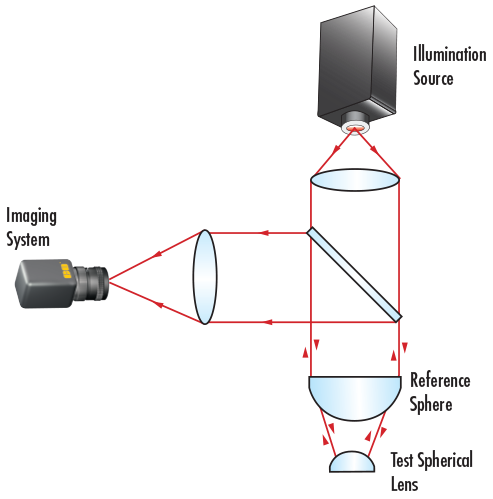
Figure 6: L'erreur sphérique est mesurée en faisant la comparaison avec une surface de référence ou en utilisant un interféromètre
L'erreur de puissance est liée à l'erreur dans le rayon de courbure par l'équation suivante. ΔR est l'erreur sur le rayon, D est le diamètre de la lentille, R est le rayon de surface et λ est la longueur d'onde (typiquement 632,8nm):
Irrégularité (Irregularity)
L'irrégularité, qui est une caractéristique de précision de surface, décrit comment la forme d'une surface s'écarte de la forme d'une surface de référence. Elle est obtenue à partir du même calcul que la planéité de surface incurvée (power). La régularité se rapporte à la sphéricité des franges circulaires qui sont formées à partir de la comparaison de la surface sous test avec la surface de référence. Lorsque la planéité (power) d'une surface est supérieure à 5 franges, il est difficile de détecter les petites irrégularités inférieures à 1 frange. Par conséquent, il est courant de spécifier des surfaces ayant un rapport de planéité/irrégularité d'environ 5:1. Pour de plus amples renseignements sur les optiques planes et l'interprétation des motifs de franges permettant de tester la planéité d'une surface plane et incurvée et son irrégularité, lire la documentation sur les Optiques Planes.
Finition de Surface
La finition de surface, également connue sous le nom de rugosité de surface, calcule les irrégularités à petite échelle sur une surface. Elles sont généralement un dérivé regrettable du processus de polissage. Les surfaces rugueuses ont tendance à s'user plus rapidement que les surfaces lisses et peuvent ne pas convenir à certaines applications, en particulier celles avec des lasers ou une chaleur intense, à cause des sites de nucléation qui peuvent apparaître dans de petites fissures ou imperfections. Les tolérances de fabrication d'une surface de finition vont de 50Å RMS pour une qualité type, à 20Å RMS pour une qualité de précision et à 5Å RMS pour une haute qualité.
CARACTÉRISTIQUES DES MATÉRIAUX
Indice de Réfraction
L'indice de réfraction d'un produit est le rapport de la vitesse de la lumière dans le vide sur la vitesse de la lumière dans le matériau. Les indices de réfraction type du verre vont de 1,4 à 4,0 et les verres pour le visible ont des indices plus bas que ceux optimisés pour l'infrarouge. Par exemple, le N-BK7 (un verre pour le visible assez prisé) possède un indice de 1,517 alors que le germanium (un élément chimique pour le IR assez prisé) possède un indice de 4,003. Pour plus d'informations sur les matériaux infrarouges, lire la documentation sur Le Matériel Adapté aux Applications Infrarouges (IR). L'indice de réfraction d'un verre optique est une propriété importante étant donné que la planéité d'une surface optique provient à la fois du rayon de courbure de la surface et de la différence dans l'indice de réfraction de chaque surface du matériau. L'Inhomogénéité, spécifiée par le fabricant de verre, décrit l'écart de l'indice de réfraction dans un verre. Elle est déterminée selon différentes classes où la classe et l'inhomogénéité sont inversement liées. L'inhomogénéité diminue alors que la classe augmente (Tableau 3).
| Tableau 3 : Caractéristiques de l'Inhomogénéité | |
|---|---|
| Classe d'Inhomonégéité | Écart Maximum Toléré de l'Indice de Réfraction |
| 0 | +/- 50 x 10-6 |
| 1 | +/- 20 x 10-6 |
| 2 | +/- 5 x 10-6 |
| 3 | +/- 2 x 10-6 |
| 4 | +/- 1 x 10-6 |
| 5 | +/- 0.5 x 10-6 |
Nombre d'Abbe
Une autre propriété du verre est le nombre d'Abbe, qui détermine la quantité de dispersion d'un verre. Il s'agit d'une fonction de l'indice de réfraction d'un matériau aux longueurs d'onde f (486,1 nm), d (587,6 nm), et c (656,3 nm) (3e équation).
Les valeurs types du nombre d'Abbe vont de 25 à 65. Les verres ayant un nombre d'Abbe supérieur à 55 (moins de dispersion) sont considérés comme des verres crown et ceux avec un nombre d'Abbe inférieur à 50 (plus de dispersion) sont considérés être des verres flint. En raison de la dispersion, l'indice de réfraction d'un verre varie avec la longueur d'onde. Ainsi, un système aura des distances focales légèrement différentes pour différentes longueurs d'onde de lumière. Pour des informations plus détaillées sur les caractéristiques importantes des matériaux tels que l'indice de réfraction et le nombre d'Abbe, veuillez lire la documentation sur Le Verre Optique.
Seuil de Dommage Laser
Le seuil de dommage laser indique la quantité maximale de puissance laser par zone, à laquelle une surface peut résister avant d'être endommagée. Les valeurs sont fournies pour des lasers pulsés et des lasers continus (CW). Le seuil de dommage laser est une caractéristique de matériau très importante pour les miroirs, étant donné qu'ils sont utilisés avec des composants laser, composants laser, plus que toute autre optique. Toutefois, toute optique d'indice laser proposera un seuil de dommage. Par exemple, considérons un Miroir Laser Ti:Saphir avec des seuils de dommage de 0,5 J/cm2 @ 150 femtosecondes d'impulsions et 100kW/cm2 CW. Cela signifie que le miroir peut résister à des densités d'énergie de 0,5 J par centimètre carré depuis un laser femtoseconde pulsé de répétition élevée, ou à 100 kW par centimètre carré depuis un laser CW haute puissance. Si le laser est concentré sur une région plus petite, une évaluation appropriée doit alors être effectuée pour s'assurer que le seuil global ne dépasse pas les valeurs spécifiées.
Bien qu'il existe toute une série de caractéristiques supplémentaire en matière de fabrication, de surface et de matériaux, la compréhension des caractéristiques optiques les plus courantes peut grandement réduire leur confusion. Les lentilles, miroirs, fenêtres, filtres, polariseurs, prismes, séparateurs, réseaux, et fibres optiques partagent ainsi une multitude d'attributs optiques communs qu'il faut savoir distinguer afin de choisir les meilleurs composants à intégrer dans les applications d'optique, d'imagerie ou de photonique sans affecter la performance globale du système.



























ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.