Exemples d'Applications Optiques

1^ère Application : Systèmes de Détection | 2^ème Application : Sélectionner la Lentille Appropriée | 3^ème Application : Élaboration d'un Système de Projection

1^ère Application : Systèmes de Détection

Chaque système optique nécessite une certaine conception préliminaire. Commencer une conception est souvent l'étape la plus intimidante, mais l'identification de plusieurs caractéristiques importantes du système permettra d'établir un plan initial. Les questions qui suivent illustrent le processus de conception d'un détecteur ou d'un système d'émetteur simple.

But : Quel Chemin Suivra la Lumière ?

Bien que les lentilles simples soient souvent utilisées dans les applications d'imagerie, dans de nombreux cas, leur objectif est de projeter de la lumière d'un point à un autre, au sein d'un système. Presque tous les émetteurs, détecteurs, lasers, et fibres optiques nécessitent une lentille pour ce type de manipulation de la lumière. Avant de déterminer le type de système à concevoir, une question importante doit être posée : "Quel chemin suivra la lumière ?" Si le but de la conception est d'obtenir toute la lumière incidente sur un détecteur, en ayant le moins d'aberrations possibles, alors une lentille simple, comme une lentille plan-convexe (PCX) ou biconvexe (DCX), peut être utilisée.

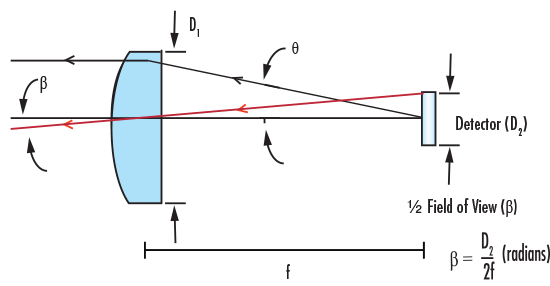
PCX Lens as FOV Limit in Detector Application

Figure 1: Lentille PCX en tant que Limite FOV dans l'Application du Détecteur

La Figure 1 montre une lentille PCX, ainsi que plusieurs caractéristiques importantes : Diamètre de la lentille (D₁) et Distance Focale (f). La Figure 1 illustre aussi de quelle manière le diamètre du détecteur limite le Champ de Vision (FOV) du système, comme montré dans l'approximation du Champ De Vision Total (FFOV) ci-dessous :

(1.1)$$ \text{FFOV} = \frac{D_2}{f} $$

Ou par l'équation exacte :

(1.2)$$ \text{FFOV} = 2 \tan^{-1}{\left( \frac{D_2}{2f} \right)} $$

Pour les détecteurs utilisés dans les systèmes de balayage, la mesure importante est le Champ De Vision Instantané (IFOV), qui est l'angle défini par le détecteur à tout instant durant le balayage.

(1.3)$$ \text{IFOV} = \frac{\text{Pixel Size}}{f} $$

Figure 2: FOV Instantané

PCX Lens as FOV Limit in Emitter Application

Figure 3: Lentille PCX en tant que Limite FOV dans l'Application de l'Émetteur

Envisagée dans le sens inverse, la Figure 1 peut également représenter un système d'émission (Figure 3), dont la lentille est utilisée pour collimater la lumière. Cette configuration sera l'hypothèse de base de l'exemple d'application.

Transmission de la Lumière : Quelle est la Quantité de Lumière au Départ ?

Savoir quel chemin prendra la lumière n'est que la première étape de la conception d'un système de projection de lumière. Il est tout aussi important de savoir quelle quantité de lumière sera transmise à partir de l'objet, ou de la source. L'efficacité est basée sur la quantité de lumière reçue par le détecteur, ce qui répond à la question "Quelle est la quantité de lumière au départ ?" L'ouverture numérique (NA) et le nombre f (f/#) d'une lentille mesurent la quantité de lumière qu'elle peut recueillir sur la base de f, D, l'indice de réfraction (n), et l'angle d'acceptation (θ). La Figure 4 illustre la relation entre le f/# et la NA.

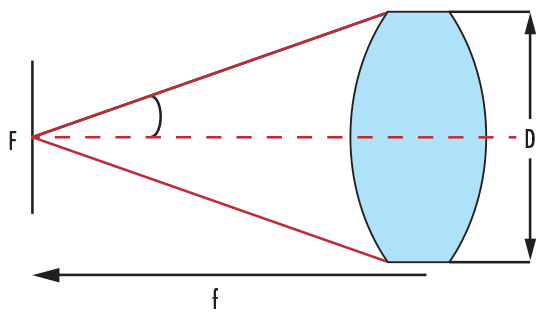
Figure 4: Lentille DCX Indiquant le f/# et la NA

Par conséquent, cette relation peut être exprimée mathématiquement selon l'Équation 1.5. Il est important de noter que plus le diamètre est large et plus le f/# est petit, ce qui permet à plus de lumière d'entrer dans le système. Pour créer le système le plus efficace qui soit, il est préférable de faire correspondre le cône de lumière émis depuis la source, au cône d'acceptation de la lentille, ce qui évite que la zone de la lentille soit trop ou trop peu remplie.

(1.4)$$ f/\# = \frac{f}{D} $$

(1.5)$$ \text{NA} = \frac{1}{2 \times f/\#} $$

(1.6)\begin{align} \text{NA} & = n \, \sin{\theta} \\ & \approx n \theta \end{align}

Rendement Optique : Quelle Quantité de Lumière Traverse le Système ?

Lorsque vous vous servez de la lentille pour transférer la lumière à partir d'un émetteur vers un détecteur, il est important de tenir compte du Rendement (TP), une mesure quantitative de l'énergie lumineuse transmise. En d'autres termes, le fait de répondre à la question "Quelle quantité de lumière traverse le système ?" détermine la géométrie de la lentille utilisée, et la configuration du système. Étant donné que les émetteurs et les détecteurs sont des zones de lumière et non sources ponctuelles, le diamètre d'une lentille modifie le TP même lorsque le rapport entre le Diamètre et la Distance Focale (spécifiée par f/#) reste constant.

La Figure 5 montre la définition de base du rendement (TP) telle qu'elle est exprimée dans l'équation 1.7, où A est la Zone de l'objet, (source lumineuse), Ω est l'Angle Solide, et z est la Distance Focale Objet (leurs conjugués dans l'espace image étant A', Ω', et z ').

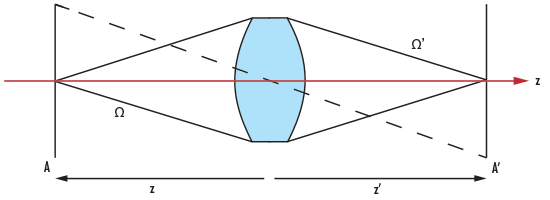
Figure 5: Lentille DCX Illustrant le Rendement

(1.7)$$ \text{TP} = n^2 A \Omega $$

L'angle solide est défini comme Ω = A/r², où A est la zone de la surface de la lentille et (r) le rayon donné comme la distance entre la lentille et l'objet (z) ou le plan d'image (z') pour respectivement Ω et Ω'.

La quantité de lumière atteignant le détecteur peut être réduite par le vignettage, qui provient du blocage physique de la lumière dans le système, en raison de contraintes dans l'ouverture de la lentille. Cependant, certains systèmes bénéficient d'un vignettage intentionnel étant donné qu'il peut éliminer la lumière parasite qui pourrait affecter la qualité de l'image. Il est important de noter qu'un alignement correct du système réduit la lumière parasite et le vignettage involontaire.

Aberrations : À Quoi Ressemble l'Image ?

Déterminer la quantité de lumière traversant le système est un facteur important. Toutefois il faut prendre également en considération des aberrations au sein du système qui peuvent jouer un rôle majeur. Répondre à la question "A quoi ressemble l'image ?" peut permettre d'améliorer la conception du système de manière à réduire les aberrations et améliorer la qualité d'image. Les aberrations sont des erreurs inhérentes à tout système optique, quelle que soit sa conception ou son alignement. Étant donné que chaque système optique contient des aberrations, l'équilibre entre la performance et le coût est une décision importante pour tout concepteur. Plusieurs aberrations élémentaires, telles que le coma (variation de l'agrandissement ou de la taille de l'image avec l'ouverture), l'aberration sphérique (rayons lumineux se focalisant devant ou derrière le foyer paraxial), et l'astigmatisme (un point focal pour les rayons horizontaux et un autre pour les rayons verticaux) peuvent être réduites par un f/# élevé, comme le montre les relations suivantes.

(1.8)$$ \text{Spherical} \propto \frac{1}{\left( f / \# \right)^3} $$

(1.9)$$ \text{Coma} \propto \frac{1}{\left( f/\# \right)^2} $$

(1.10)$$ \text{Astigmatism} \propto \frac{1}{\left( f / \# \right)} $$

Exemple d'Application : Système de Détection

À titre d'exemple, imaginez un système dans lequel la lumière est émise à partir d'un guide lumineux en fibre optique, de diamètre ¼", comme dans la Figure 3.

Paramètres Initiaux
NA du Guide Lumineux = 0,55
Diamètre de la Source (Émetteur) = 6,35 mm
Indice de Réfraction de l'Air = 1
Paramètres Calculés
Nombre f (f/#)

(1.11)\begin{align} \text{NA} & = \frac{1}{2 \times \left( f /\# \right)} \\ 0.55 & = \frac{1}{2 \times \left( f /\# \right)} \\ f /\# & = 0.9 \end{align}

Il serait idéal de placer une lentille PCX de f/1, ce qui signifie que le nombre f (f/#) est de 1, en face du guide lumineux pour collimater autant de lumière que possible. Conformément à l'Équation 1.4, si le f/# est de 1, alors le diamètre et la distance focale d'une lentille sont égaux. En d'autres termes, si l'on considère une lentille d'un diamètre de 12 mm, alors la distance focale est également de 12 mm.

Champ De Vision Total (FFOV)

(1.12)\begin{align} \text{FFOV} & = \frac{D_2}{f} \\ \text{FFOV} & = \frac{D_{\text{Source}}}{f_{\text{Lens}}} \\ & = \frac{6.35 \text{mm}}{12 \text{mm}} = 0.529 \text{ radians} \end{align}

(1.13)\begin{align} A_{\text{Source}} & = \pi r^2 \\ & = \pi \left( \frac{6.35 \text{mm}}{2} \right)^2 = 31.669 \text{mm}^2 \end{align}

(1.14)\begin{align} A_{\text{Lens}} & = \pi r^2 \\ & = \pi \left( \frac{12 \text{mm}}{2} \right)^2 = 113.097 \text{mm}^2 \end{align}

(1.15)\begin{align} \Omega & = \frac{A_{\text{Lens}}}{r^2} \\ & = \frac{113.097 \text{mm} ^2}{\left( 12 \text{mm} \right)^2} = 0.7854 \text{ steradians} \end{align}

Le stéradian correspond à un angle bi-dimensionnel dans un espace tri-dimensionnel, étant donné que l'angle de bord à bord de la lentille a deux dimensions. Une valeur plus élevée en stéradian est donnée par une distance plus courte entre l'émetteur et la lentille, ou par un plus grand diamètre de la lentille. La plus grande valeur qu'un angle solide puisse avoir est de 4π, soit environ 12,57, ce qui serait équivalent à l'angle solide de tout l'espace.

Pour calculer le Rendement (TP) de ce système, nous devons d'abord calculer la Surface de la Source (Équation 1.11), la Surface de la Lentille (Équation 1.12) et l'Angle Solide (Équation 1.13). Une règle de base pour collimater la lumière provenant d'une source divergente (c.-à-d. le guide lumineux dans cet exemple), est de placer la lentille à la distance égale à la distance focale éloignée de la source.

(1.16)\begin{align} \text{TP} & = n^2 A \Omega \\ & = \left( 1 \right) \left( 31.669 \text{mm}^2 \right) \left( 0.7854 \text{ steradians} \right) \\ & = 24.873 \text{mm}^2 \, \text{ steradians} \end{align}

Le système étant dans l'espace libre, où n est considéré être 1, n² n'est pas pris en compte dans le calcul final.

2^ème APPLICATION : SÉLECTIONNER LA LENTILLE APPROPRIÉE À VOTRE BESOIN

Une image de haute qualité est synonyme de faibles aberrations. Par conséquent, les concepteurs utilisent souvent deux ou plusieurs lentilles afin d'obtenir une qualité d'image supérieure par rapport à une solution à une seule lentille. De nombreux facteurs tels que le type de la source, les contraintes d'espace, le coût, etc... contribuent à la sélection de la lentille appropriée à votre besoin.

Les Figures 6a à 6e comparent une multitude de systèmes de lentilles pour un objectif relai ou d'imagerie 1:1. Dans cet exemple précis, décrit dans la série de comparaisons suivante, il est facile de voir comment la qualité d'image est affectée par la géométrie et les propriétés optiques inhérentes aux lentilles choisies.

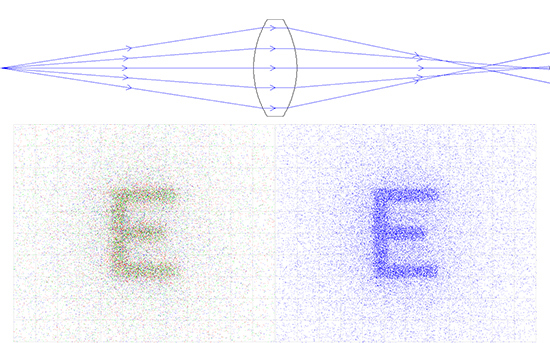
Figure 6a: Système Relais avec Lentille DCX. EFL de 25 mm et 20 mm de Diamètre de la Pupille d'Entrée (Couleur à Gauche et Monochromatique à Droite)

Figure 6b: Système Relais avec Lentilles PCX. EFL de 50 mm et 20 mm de Diamètre de la Pupille d'Entrée (Couleur à Gauche et Monochromatique à Droite)

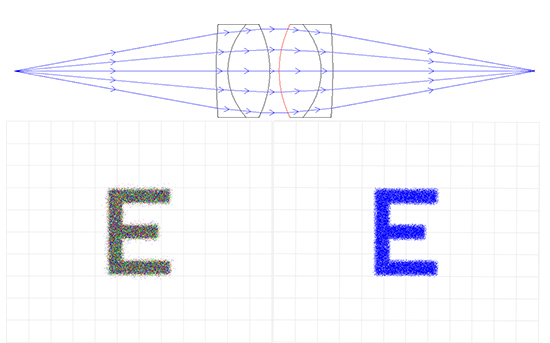
Figure 6c: Système Relais avec Lentilles Achromatiques. EFL de 50 mm et 20 mm de Diamètre de la Pupille d'Entrée (Couleur à Gauche et Monochromatique à Droite)

Figure 6d: Système Relais avec Lentilles Achromatiques Asphérisées. EFL de 50 mm et 50 mm de Diamètre de la Pupille d'Entrée (Couleur à Gauche et Monochromatique à Droite)

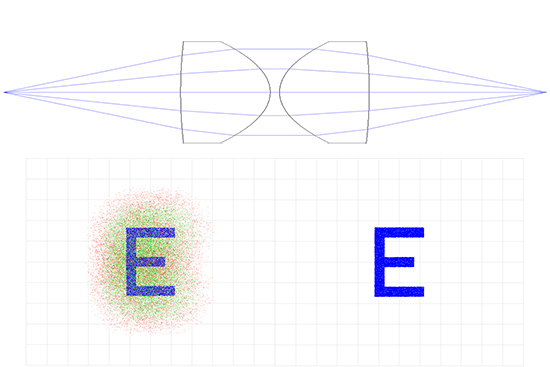
Figure 6e: Système Relais avec Lentilles Asphériques. EFL de 50 mm et 40 mm de Diamètre de la Pupille d'Entrée (Couleur à Gauche et Monochromatique à Droite)

Exemple d'Application : Système de Lentille à Un Seul Élément

Une lentille biconvexe (DCX) est considérée comme l'unique meilleur élément de l'imagerie 1:1 en raison de sa forme symétrique où les deux surfaces symétriques de la lentille ont le même pouvoir réfringent. Ce qui n'est pas le cas avec une lentille plan-convexe (PCX) où la surface courbée focalise les rayons davantage. Étant donné que le système de lentilles est constitué que d'une seule lentille, le diaphragme d'ouverture est essentiellement la lentille, ce qui permet de réduire de nombreuses aberrations. Pour ces raisons, une lentille DCX est préférable à une seule lentille PCX pour l'imagerie 1:1. Il est cependant important de garder à l'esprit qu'à un faible f/#, il existe encore une aberration sphérique et un coma importants. Ces aberrations sont causées par le Facteur de Forme (S) de la lentille unique :

(2.1)$$ S = \frac{R_2 + R_1}{R_2 - R_1} $$

où R₁ et R₂ sont les rayons de chaque surface de la lentille.

Pour les applications dont l'objet ou la source est à l'infini et qui ne nécessitent qu'une seule lentille, un meilleur facteur de forme peut être trouvé afin de réduire l'aberration qui pourrait endommager le système. Par exemple, pour réduire l'aberration sphérique, le facteur de forme idéal peut être calculé par :

(2.2)$$ S = -\frac{ 2 \left( n^2 - 1 \right) }{n + 2} p $$

(2.3)$$ S = \frac{R_2 + R_1}{R_2 - R_1} $$

(2.4)$$ p = \frac{z' + z}{z' - z} $$

avec n l'Indice de Réfraction du Substrat de Verre, p le Facteur de Position, z la Distance Objet (mesurée à une valeur négative), et z' la Distance Image (mesurée à une valeur positive).

Pour réduire le coma d'un objet à l'infini, le Facteur de Forme peut être calculé par :

(2.5)$$ S = - \frac{\left( 2n^2 - n - 1 \right)}{n + 1} p $$

Pour le verre ayant un indice de 1,5 (le N-BK7 est de 1,517), avec un objet situé à l'infini, un Facteur de Forme d'environ 0,8 équilibrera les corrections des aberrations sphériques et du coma.

Exemple d'Application : Système de Lentilles à Deux Éléments

Pour améliorer le système, une lentille DCX unique pourrait être remplacée par deux lentilles PCX égales, ayant chacune une distance focale de deux fois celle de la lentille DCX et un diaphragme d'ouverture situé au centre. Cela permet de répartir le pouvoir réfringent de chaque surface des lentilles, étant donné que la distance focale est inversement proportionnelle au pouvoir réfringent. Vu que chaque lentille a un pouvoir réfringent plus faible, l'aberration sphérique créée dans le système est moindre. En utilisant deux lentilles, le pouvoir réfringent de chaque surface s'ajoute, ce qui permet d'avoir la même distance focale globale, mais une aberration sphérique moindre. Comme le diamètre reste également le même, le f/# n'a pas changé entre l'utilisation d'une DCX unique ou de deux lentilles PCX, mais l'aberration sphérique a diminué, même si le f/# est plus grand.

Les surfaces convexes sont presque en contact avec le diaphragme d'ouverture disposé entre les deux. Une meilleure qualité d'image est obtenue en orientant les surfaces convexes vers la plus longue distance conjuguée.

Exemple d'Application : Système de Lentille Achromatique

Une autre option consiste à utiliser deux lentilles achromatiques, ou achromats. Une lentille achromatique est constituée de deux composants optiques cimentés ensemble, généralement d'un élément positif à faible indice (crown) et d'un élément négatif à haut indice (flint). L'utilisation d'achromats améliore l'imagerie polychromatique (lumière blanche, longueurs d'onde multiples) tout en réduisant l'aberration sphérique et le coma. Si les deux lentilles sont des achromats avec des surfaces convexes se faisant face, on obtient un système d'imagerie nettement supérieur étant donné que de nombreuses aberrations sont considérablement réduites par rapport au même système avec des lentilles simples (DCX ou deux PCX). Tandis que l'aberration sphérique est négligeable avec de grandes ouvertures ou des nombres f/# élevés, l'aberration chromatique est grandement réduite avec l'utilisation d'achromats. De nombreux systèmes d'objectifs relai sur le marché, utilisent ce type de configuration à quatre éléments.

Pour plus d'informations sur les avantages de l'utilisation de lentilles achromatiques comparées aux singulets, lire Pourquoi Utiliser une Lentille Achromatique ?.

Exemple d'Application : Système de Lentille Asphérique

Contrairement aux lentilles PCX, DCX et achromatiques, qui sont fabriquées à partir de sphère, une lentille asphérique possède une courbure différente de celle d'une sphère ou d'un cylindre, constituée généralement à partir d'une hyperbole ou d'une parabole. Le concept clé des lentilles asphériques, ou asphères, est que le rayon de courbure varie radialement de l'axe optique de la lentille. Par conséquent, les lentilles asphériques corrigent facilement l'aberration sphérique, et sont parfaites pour corriger les aberrations hors axe.

Les lentilles asphériques sont utilisées dans de nombreux systèmes, car une lentille asphérique cpeut remplacer deux ou plusieurs lentilles sphériques, ce qui réduit l'espace et les coûts dans un système. Pour plus d'informations sur la fabrication, la conception et l'utilisation de lentilles asphériques, lire Tout sur les Lentilles Asphériques.

Type de Système de Lentille	Aberration Sphérique	Aberration Chromatique
Singulet DCX	Élevée	Élevée
2 PCX	Moyenne	Élevée
2 Achromats	Faible	Négligeable
2 Aspherized Achromats	Négligeable	Négligeable

3^ème APPLICATION : ÉLABORATION D'UN SYSTÈME DE PROJECTION

La conception d'un système de projecteur personnalisé peut souvent prendre beaucoup de temps et s'avérer coûteux. Néanmoins, quelques étapes simples à suivre peuvent rendre le processus facile et rentable. Les mêmes étapes élémentaires peuvent s'appliquer à de nombreuses applications de conception de système.

Étapes de Conception sur Mesure :

Diviser le Système en Plusieurs Parties – Les applications optiques sont nombreuses et variées, allant de simples loupes au conditionnement de faisceaux laser. La plupart des applications peuvent toutefois être décomposées en de plus petits modules pouvant être développés de manière quasi indépendante.
Concevoir Chaque Partie Séparément – En prenant chaque module et en le concevant pour une performance individuelle optimale, cela peut être bénéfique pour le système tout entier. Cela est vrai tant que l'optimisation d'un module n'a pas d'effet négatif sur la conception d'un autre module, aussi il est important de garder l'ensemble du système à l'esprit lorsque vous concevez des parties séparées.
Optimiser le Calcul – Après le calcul des dimensions initiales, introduire le design dans un logiciel de conception optique, comme ZEMAX ou Code V, est la meilleure façon d'optimiser les modules indépendamment ainsi que la conception globale. L'optimisation de chaque module du système donnera le meilleur scénario possible à partir duquel des éléments de fixation appropriés pourront être choisis. Cela sert aussi de double vérification pour veiller à ce que les calculs produisent des données raisonnables.
Assembler le Système – Après la conception de chaque module, l'ensemble du système doit être construit. Avant de rassembler les modules, il est nécessaire de les vérifier individuellement pour garantir qu'ils fonctionnent correctement et peuvent être ajoutés au système. Une fois le système est établi, il est préférable d'exécuter également l'ensemble du système via le logiciel de conception optique, afin de s'assurer que les modules fonctionnent ensemble correctement dans le système.
Sélectionner les Parties – La plupart des progiciels de conception optique comprennent une bibliothèque des prescriptions de lentilles en stock et un algorithme de meilleure concordance qui permet d'introduire de vrais lentilles et éléments à la place de pièces sur mesure. Le logiciel de conception optique permet d'optimiser un certain nombre de verres qui peuvent ne pas exister, mais la meilleure concordance donnera un type de verre très semblable qui pourra ensuite être acheté. Au-delà du choix des verres appropriés, la recherche de la mécanique adaptée au système est une étape importante. La taille, le poids et l'apparence doivent être considérés avant de choisir des supports de lentilles et des systèmes de monture.

Pour plus d'informations sur la sélection du verre, lire Verre Optique.

La plupart des projecteurs, tels que les projecteurs de diapositives à l'ancienne, utilisent deux principaux modules : un système de lentille condenseur et un système de lentille projecteur. Le système de lentille condenseur illumine uniformément une diapositive tandis que le système de lentille projecteur projette une image de la diapositive sur un écran. Chaque module peut être créé avec des composants et des méthodes simples. Une optique de 25 mm de diamètre sera utilisée dans cet exemple, en raison de sa grande ouverture et d'une grande variété de distances focales disponibles.

1^ère Partie : Le Système de Lentilles de Projection

Le système de lentilles de projection est limité par le grossissement désiré et la distance de projection de l'image d'un réticule. Étant donné que la plupart des systèmes de projection utilisent la lumière blanche, l'utilisation de lentilles achromatiques donnera la meilleure image. Pour savoir quels sont les achromats à utiliser, vous devez déterminer la distance à la laquelle se situera le système de lentille de projection et le grossissement désiré (M) à partir de l'image projetée (I). Le grossissement peut être calculé par les distances focales des lentilles (Équation 3.1) ou par la distance de l'image vers l'objet (Équation 3.2).

(3.1)$$ M = \frac{F_2}{F_1} $$

(3.2)$$ M = \frac{I}{O} $$

2^ème Partie : Le Système de Lentilles Condenseur

Le système de lentilles condenseur recueille la lumière à partir de sources lumineuses divergentes, puis redirigent et condensent la lumière pour illuminer le système de lentille projecteur. Le système de lentille condenseur classique est constitué de deux lentilles PCX montées avec leurs surfaces convexes se faisant face, comme le montre la Figure 7. La première lentille recueille le cône lumineux divergent de l'illuminateur (objet ou projecteur) et la seconde lentille restitue la lumière comme un cône convergent (image) illuminant le réticule.

Figure 7: Système de Projection Élémentaire

Implicitement, la solution du système de lentilles de projection définit une partie du système de lentilles condenseur, ce qui explique pourquoi il est crucial de concevoir le système de lentille de projection en premier. La distance entre le système de lentilles condenseur et le système de lentilles de projection est au moins aussi grande que la distance du réticule au système de lentilles de projection.

Exemple d'Application : Conception d'un Système de Projection

Paramètres Initiaux
Diamètre de la Lentille = 25 mm
Distance de l'Image = Distance de Projection = 250 mm
Grossissement = 2,5X
Paramètres Calculés
Distance Objet ou Distance au Réticule

(3.3)\begin{align} M & = \frac{F_2}{F_1} \\ 2.5 & = \frac{250 \text{mm}}{F_1} \\ F_1 & = \frac{250 \text{mm}}{2.5} = 100 \text{mm} \end{align}

Deux lentilles achromatique de distance focale 100 mm, ayant un diamètre de 25 mm, seraient parfaites pour la création d'un système de lentilles de projection. Les lentilles de 25 mm de diamètre sont parfaites en raison de leurs grandes ouvertures et de leur compatibilité avec les composants mécaniques, ainsi que pour leur variété de traitements et de distances focales.

Distance Focale de la Lentille Condenseur PCX

(3.4)\begin{align} M & = \frac{F_2}{F_1} \\ F_2 & = M \cdot F_1 = \left( 2.5 \text{X} \right) \left( 100 \text{mm} \right) = 250 \text{mm} \end{align}

Deux lentilles PCX ayant une distance focale de 250 mm et un diamètre de 25 mm sont requises pour réaliser le système de projection.

Ce contenu vous a-t-il été utile ?

Merci d'avoir évalué ce contenu !