Effets de la planéité de la surface de miroirs laser

Les systèmes laser nécessitent souvent des composants optiques extrêmement précis, tels que des miroirs et des lentilles, dont les spécifications approchent les limites de ce qu'il est possible de fabriquer. Lors de la création d'un système optique dans lequel un laser sera utilisé, il est important de prendre en compte les attentes quant à ce qui peut être fabriqué au niveau de prix souhaité. Comprendre quels facteurs de performance sont cruciaux par rapport à ceux qui sont souhaités, mais inutiles, permet de gagner du temps et de l'argent. Selon l'application, un système laser peut ou non nécessiter des composants optiques personnalisés de haute performance. Cette note d'application démontre ce point en explorant les effets simulés de la planéité de la surface du miroir sur la taille du point focalisé d'un faisceau laser gaussien d’entrée se propageant dans un système simulé de traitement des matériaux par laser.

Cette note d'application a des implications pour tout système laser comprenant un ou plusieurs miroirs laser. Pour maximiser l'efficacité des systèmes laser, les miroirs des lasers sont généralement recouverts d'un traitement par pulvérisation ionique (IBS) ou par évaporation. Les traitements IBS sont des types de traitements pour miroirs très appréciés en raison de leur performance spectrale extrêmement élevée, ce qui signifie qu'ils peuvent atteindre des réflectivités très élevées. Cependant, ils exercent une très forte contrainte sur la surface sur laquelle ils sont appliqués, ce qui risque de déformer la surface du miroir, à moins d'appliquer un traitement compensateur au dos de l'optique ou de procéder à un recuit prolongé. Les traitements évaporatifs n'appliquent qu'une faible contrainte à la surface du miroir, mais leur performance spectrale est inférieure à celle des traitements IBS. Bien que cette note d'application n'explore pas directement les effets des traitements, les courbures simulées des miroirs sont proches des courbures conférées aux miroirs par les contraintes symétriques d'un traitement IBS.

Limites et directives optiques

Rayon de courbure

La planéité et la courbure de la surface font toutes deux référence à la forme de la surface d'un miroir. Alors que la planéité de la surface est la déviation de la surface par rapport à sa forme nominale, la courbure est définie comme l'inverse du rayon de courbure (équation 1).

(1)$$ C = \frac{1}{R} $$

Comme cette simulation nécessite l'entrée du rayon de courbure, R, il doit être déterminé à partir de plusieurs autres dimensions et propriétés du miroir. On suppose d'abord que le miroir aura une courbure sphérique, ce qui est souvent le cas pour les traitements sous contrainte, et que le sag maximal, abréviation de sagitta, sera exactement égal à la planéité de la surface, SF (équation 2).

(2)\begin{align} \text{sag} & = \text{SF} \left[ \text{waves} \right] \\ & = \text{SF} \left[ \lambda \right] \end{align}

Dans le cas où un faisceau est réfléchi par un seul miroir, la planéité de la surface sera également égale à l'erreur du front d'onde réfléchi, ou distorsion du front d'onde. La planéité de la surface est généralement indiquée en unités de franges ou d'ondes et, en tant que telle, la planéité de la surface d'un miroir est indiquée comme une fraction réelle positive ou un multiple entier de la longueur d'onde de la lumière utilisée avec le miroir. L'expansion de l'équation pour le sag nécessite une attention précise à la sémantique. L'équation 3 nécessite le demi-diamètre de l'ouverture utile du miroir, ρ, qui est également connu comme le demi-diamètre utile.

(3)$$ R - \sqrt{R^2 - \rho^2} = \text{SF} $$

Cette distinction est importante pour une simulation précise dans Zemax OpticStudio, car il existe également un semi-diamètre mécanique, qui correspond simplement à la moitié du diamètre de l'optique et ne tient pas compte de l'ouverture utile. La planéité de la surface et le demi-diamètre utile permettent de déterminer le rayon de courbure (équation 4).

(4)$$ R = \frac{1}{2} \left[ \text{SF} + \frac{\rho ^2}{\text{SF}} \right] $$

Comme le sag du miroir est de plusieurs magnitudes plus petites que le rayon du miroir, la contribution du premier terme au rayon de courbure est négligeable. Il est donc raisonnable d'utiliser l'approximation parabolique pour simplifier l'équation 4 en équation 5.

(5)$$ R \approx \frac{1}{2} \times \frac{\rho ^2}{\text{SF}} $$

La courbure étant inversement proportionnelle au rayon de courbure, la courbure est directement proportionnelle à la planéité de la surface. Il est important de faire cette distinction car la courbure du miroir sera modifiée en changeant uniquement la planéité de la surface dans cette note d'application. Par exemple, un miroir d'un diamètre de 25 mm a un demi-diamètre mécanique de 12,5 mm. Avec une ouverture utile de 85%, le demi-diamètre utile (ρ) du miroir est de 10,625 mm. Avec une planéité de surface de λ/10 et une longueur d'onde de 1064 nm, le rayon de courbure est d'environ 5,3 × 105 mm et la courbure est de 1,9 × 10^-6 mm.

La limite de diffraction

La limite de diffraction du point focalisé, décrite par l'équation de la tache d'Airy, peut être utilisée pour déterminer la limite inférieure à laquelle la taille du point du diamètre d'un faisceau peut être focalisée, désignée par d et étant donné la longueur d'onde de la lumière, λ, la distance focale de la lentille convergente, f, et la taille ou le diamètre du faisceau, D. Cette limite inférieure est déterminée en supposant que la lentille convergente est une lentille parfaite, paraxiale et sans aberration (équation 6).

(6)$$ d \approx 2,44 \frac{f \, \lambda }{D} $$

Par exemple, un faisceau laser de 1064 nm d'un diamètre de 5 mm étant focalisé par une lentille paraxiale de 100 mm de distance focale, a un diamètre de la tache d'Airy d'environ 52 μm. Un faisceau de lumière ne peut pas être focalisé plus petit sans l'utilisation d'une lentille plus puissante. Cependant, comme les lentilles paraxiales parfaites et sans aberration n'existent pas vraiment, la taille du point sera probablement supérieure à cette valeur. L'équation de la tache d'Airy fournit simplement la limite inférieure, appelée limite de diffraction, à laquelle une taille de point peut être focalisée.

Simulation et résultats de Zemax OpticStudio

La simulation utilisée pour tester les effets de la courbure du miroir sur la taille du faisceau focalisé a été créée dans Zemax OpticStudio 18.9. Le modèle utilise un faisceau gaussien de 2,5 mm de diamètre et d'une longueur d'onde donnée traversant un système composé de six miroirs identiques (ayant les mêmes diamètres et planéités de surface) et de trois lentilles Edmund Optics, comme le montre la Figure 1.

Ce système d'expansion de faisceau simulé comporte six miroirs identiques à courbure variable, les lentilles PCV #48-049 et PCX #48-281 pour l'expansion de faisceau 5X, et la lentille PCX #37-817 comme la lentille condenseur

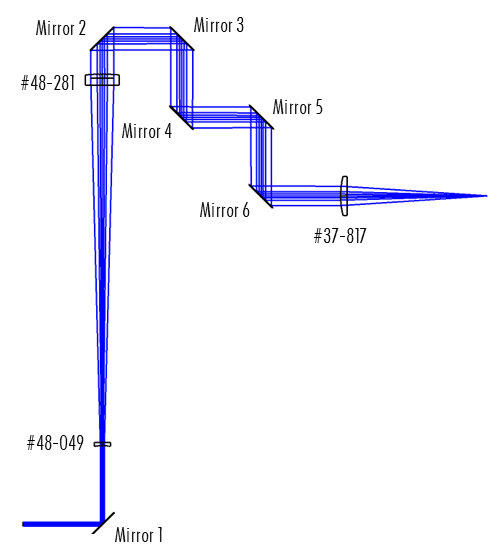
Figure 1 : Ce système d'expansion de faisceau simulé comporte six miroirs identiques à courbure variable, les lentilles PCV #48-049 et PCX #48-281 pour l'expansion de faisceau 5X, et la lentille PCX #37-817 comme lentille condenseur

Dans cette simulation, les miroirs ont été dotés de demi-diamètres mécaniques de 12,5 mm et de semi-diamètres utiles de 10,625 mm pour respecter la convention, qui conseille que l'ouverture utile d'une optique soit égale à 85 % de son diamètre. Ce diamètre a été choisi pour garantir que le faisceau de rayons se trouve dans l'ouverture libre de la deuxième lentille de l'expanseur de faisceau, bien que dans une application réelle, des diamètres beaucoup plus grands seraient choisis pour cette taille de faisceau afin d'éviter l'écrêtage du faisceau gaussien. L'expanseur de faisceau 5X était composé des lentilles Edmund Optics #48-049 et #48-281. Les miroirs 2 à 6 ont été placés à 50 mm l'un de l'autre pour replier le chemin optique, simulant ainsi les contraintes d'espace dans un système laser réel. La distance entre les deux lentilles constituant l'expanseur de faisceau, ainsi que la distance entre le dernier miroir et la lentille du condenseur, ont été optimisées pour focaliser le faisceau au niveau du plan de focalisation final afin d'obtenir les tailles géométriques (GEO) des points pour le faisceau focalisé à des courbures de miroir variées.

Afin d'évaluer la taille du point à différentes valeurs de planéité de la surface, mais à la même longueur d'onde, la planéité de la surface a été définie comme un multiple positif en nombre réel de la longueur d'onde, et ce multiple a été augmenté. Ce multiple sera appelé le coefficient de courbure, C', pour simplifier. Ce coefficient de courbure, qui est une valeur sans unité, ne doit pas être confondu avec la courbure, qui est l'inverse du rayon de courbure et a des unités de longueur, comme indiqué dans l'équation 1. La courbure peut également s'étendre sur plusieurs magnitudes, tandis que le coefficient de courbure, qui peut être un nombre positif quelconque, est généralement une fraction inférieure à 1. Ainsi, le sag peut être représentée comme la longueur d'onde de la lumière dans le système, λ, multipliée par le coefficient de courbure (équation 7).

(7)\begin{align} C' & \in \mathbb{R}_{\geq 0} \\ \text{SF} \left[ \lambda \right] & = C' \\ \text{SF} \left[ \text{nm} \right] & = C' \times \lambda \end{align}

Les résultats respectifs pour trois longueurs d'onde et neuf valeurs de coefficients de courbure sont présentés dans le Tableau 1 et la Figure 2.

	Taille des points GEO (μm)
Planéité de surface (P - V)	0λ	λ/20	λ/10	λ/8	λ/4	λ/2	1λ	2λ	5λ
1064 nm	22,4	22,9	25,1	26,3	32,0	43,7	67,2	116,4	270,8
532 nm	21,7	21,6	22,3	22,8	25,6	31,3	42,9	66,1	139,0
355 nm	20,7	21,6	21,6	21,9	22,7	26,5	34,1	34,1	96,1

Tableau 1 : Tailles des points simulées pour une courbure croissante du miroir à 1064 nm et aux deux premières longueurs d'onde de l'harmonique Nd:YAG

Figure 2 : La taille des points géométriques du Tableau 1 augmente rapidement à mesure que les miroirs deviennent plus courbes

La Figure 2 montre que les tailles des points focalisés pour des miroirs présentant une planéité de surface λ/20 à l'échelle de 300 μm semblent être presque exactement les mêmes. Lorsque la planéité de la surface diminue, la taille des points focalisés devient plus grande comme pour les grandes longueurs d'onde. Après une planéité de surface de λ/4, la taille du point focalisé commence à augmenter plus sensiblement pour toutes les longueurs d'onde.

Principaux effets et recommandations

En réalité, il n'existe pas de miroirs parfaitement plats. Si les spécifications de planéité de la surface sont moins strictes (augmentation de la courbure du miroir), la taille du point augmente et le front d'onde réfléchi se dégrade. Lorsque le profil de la surface d'un miroir varie de manière significative par rapport à sa forme nominale, il peut être utile d'ajuster les aberrations de la surface à un ensemble de fonctions appelées polynômes de Zernike. Selon le profil exact de la surface du miroir et les angles auxquels les miroirs sont positionnés par rapport au faisceau incident, les effets d'aberration des lentilles et des miroirs en aval peuvent s'agréger de manière constructive ou destructive.

Dans cette simulation, pour des raisons de simplicité, les miroirs ont été traités comme étant uniquement sphériques ou plats. En conséquence, les profils des faisceaux sont devenus moins circulaires et plus étalés. Il est toutefois important de noter que des aberrations sphériques étaient présentes à l'origine dans l'expanseur de faisceau et les lentilles de focalisation du faisceau et que les effets ont inévitablement été transportés dans le système et déformés par l'inclinaison et la courbure sphérique des miroirs. Ces interactions étant complexes et pouvant être potentiellement additives ou soustractives selon l'emplacement des miroirs, l'optimisation de l'espacement des lentilles par OpticStudio était nécessaire pour minimiser les effets d'aberration et focaliser le point. Un autre facteur non pris en compte est l'utilisation de traitements optiques.

Il est également important de ne pas négliger la façon dont la longueur d'onde de la lumière, associée à la courbure du miroir, affecte la taille et la forme du point. Aux grandes longueurs d'onde, les écarts de taille et de forme des points sont plus importants et semblent plus prononcés qu'aux petites longueurs d'onde (Figure 3).

La taille du point focalisé d'un faisceau de 1064 nm à des coefficients de courbure croissants à trois échelles : 600 μm (haut), 200 μm (milieu) et 100 μm (bas)

Figure 3 : La taille du point focalisé d'un faisceau de 1064 nm à des coefficients de courbure croissants à trois échelles : 600 μm (haut), 200 μm (milieu) et 100 μm (bas)

Cette simulation étant strictement théorique, chaque miroir et chaque lentille ont respectivement réfléchi et transmis 100% de la lumière incidente. En réalité, les systèmes laser utilisent des traitements réfléchissants très performants pour maximiser la réflexion des miroirs et des traitements antireflets pour maximiser la transmission des lentilles. Ces traitements ont toutefois des longueurs d'onde ou des plages de longueurs d'onde spécifiques et des seuils de dommage laser (LIDT) qui doivent être pris en compte pour les systèmes réels.

Il convient de noter qu'un grand nombre de spécifications et de facteurs peuvent déterminer les performances du système et les coûts de fabrication, comme les types de traitement ou les spécifications mécaniques telles que le parallélisme ou la précision de la surface. Ces facteurs supplémentaires sont tout aussi importants à prendre en compte lors de la sélection des composants d'un système laser, même si beaucoup d'entre eux seront omis dans l'essentiel de cette simulation.