Choisir la bonne mire de test

Composants de la qualité de l'image | Profondeur de champ | Types de mires de test | Exemples d'application

Les mires de test sont utiles pour évaluer ou calibrer les performances ou la qualité d’image d'un système d'imagerie. Il peut s'agir de dépanner un système, de certifier ou d'évaluer des mesures, ou d'établir une base pour garantir qu’un système fonctionnent bien avec un autre. La qualité de l'image peut être définie par différents éléments, en particulier la résolution, le contraste, la fonction de transfert de modulation (FTM), la profondeur de champ (DOF) et la distorsion ; par conséquent, un ou plusieurs types de mires de test peuvent être nécessaires ou utiles en fonction du type de système en cours de construction ou de ce qui doit être mesuré. Heureusement, il existe un éventail de mires qui s'adressent à des systèmes spécifiques, notamment les caméras, les écrans de visualisation ou même une seule et fine lentille. Pour pouvoir choisir la bonne mire de test, il est important de comprendre d'abord les composantes de la qualité de l'image.

COMPOSANTES DE LA QUALITÉ DE L'IMAGE

Résolution

La résolution est la capacité d'un système d'imagerie à distinguer les détails d'un objet. Elle est souvent exprimée en termes de paires de lignes par millimètre (lp/mm) (voir Figure 1). Une image à faible résolution manque généralement de détails fins et est souvent floue, alors qu'une image à haute résolution est très détaillée et claire.

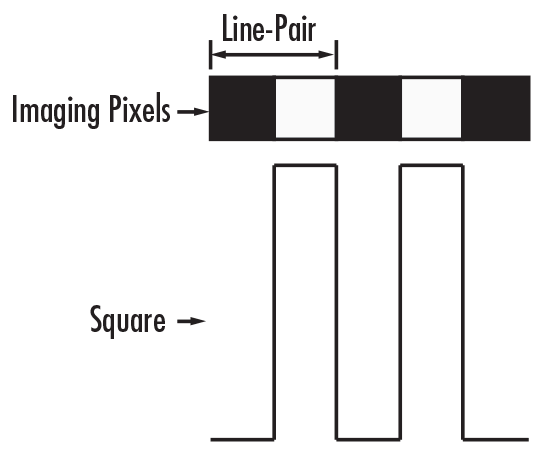
Figure 1 : Relation entre les paires de lignes et les ondes carrées

Pour illustrer ce concept, imaginons que deux carrés soient représentés sur les pixels d'une caméra CCD. En supposant que le grossissement primaire de l'objectif soit tel qu'un carré remplisse un pixel de la caméra (Figure 2a), s'il n'y a pas d'espace entre les pixels remplis, l'image apparaîtra comme un grand rectangle rouge. Toutefois, si un « espace blanc », ou un espace distinctement différent de la couleur originale du pixel, est trouvé entre les pixels, la caméra sera en mesure de distinguer les deux carrés (Figure 2b). Par conséquent, l'association du carré rouge et de « l'espace blanc » devient une lp/mm, ce qui correspond à deux pixels distincts.

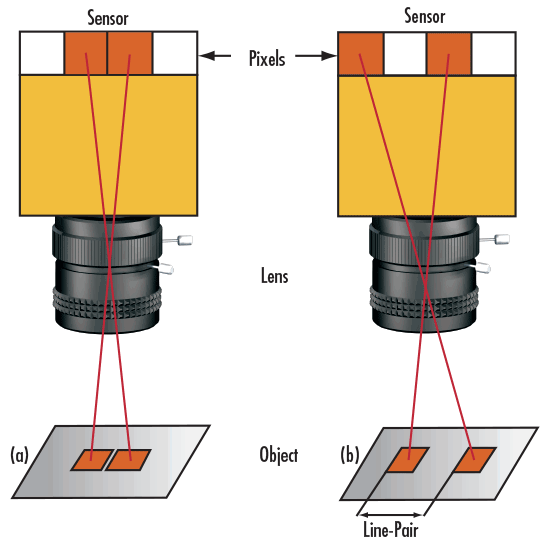
Figure 2 : Paire de carrés rouges non résolus (a) vs. résolus (b)

Contraste

Le contraste mesure la séparation entre les zones claires et sombres d'une image. Plus précisément, le contraste est un changement d'intensité ou de luminosité d'un point à un autre. Il affecte l'efficacité de la reproduction des différences entre l'objet et les nuances de gris de l'arrière-plan. Une image présentant le contraste le plus élevé est une image dans laquelle le noir est vraiment noir et le blanc vraiment blanc, sans aucune nuance de gris entre les deux. Lorsque le contraste diminue, la distinction entre le noir et le blanc commence à s'estomper, au sens littéral du terme, et des nuances de gris apparaissent (Figure 3).

Figure 3 : Le contraste par rapport aux pixels

Le contraste est souvent exprimé en pourcentage (%) et est calculé en utilisant l'intensité maximale (I_max) et l'intensité minimale (I_min), comme indiqué dans l'équation 1. Il peut également être représenté par une fonction périodique (onde carrée ou sinusoïdale), ou une fonction qui alterne régulièrement et instantanément entre deux niveaux.

Fonction de transfert de modulation (FTM ou MTF)

La fonction de transfert de modulation, FTM, est une mesure de la capacité d'un objectif d'imagerie à transférer le contraste du plan de l'objet au plan de l'image à une résolution spécifique. Les plans de l'objet et de l'image sont les zones spatiales où se trouvent l'objet et l'image. Le plan de l'objet se trouve devant le système d'imagerie, et le plan de l'image se trouve devant ou derrière le système d'imagerie, selon que l'image est réelle ou virtuelle. La FTM est exprimée en fonction de la résolution de l'image (lp/mm) et du contraste (%), comme le montre la figure 4. En règle générale, à mesure que la résolution augmente, le contraste diminue jusqu'à un point limite où l'image devient irrésolue et grise.

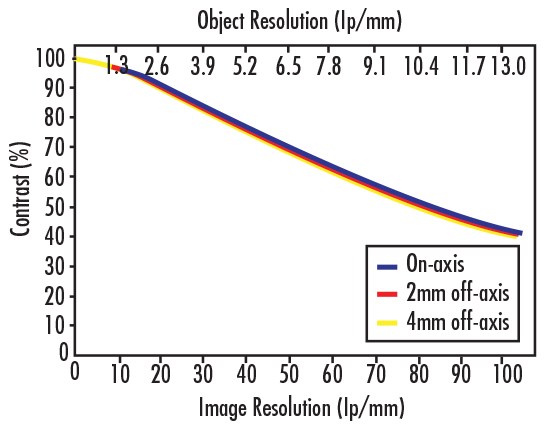
Figure 4 : Exemple de courbe FTM d'un objectif d'imagerie PMAG 0,13X

Une autre composante de la FTM, outre la résolution et le contraste mentionnés ci-dessus, est la limite de diffraction. La limite de diffraction est une limite physique qui empêche un objectif d'imager parfaitement des points ou des bords. Étant donné qu'elle est limitée par la nature ondulatoire de la lumière, même une lentille « parfaitement » conçue et fabriquée ne peut pas atteindre des performances limitées par la diffraction. Cependant, les concepteurs utilisent diverses méthodes pour réduire les aberrations et augmenter la précision globale du système afin de s'approcher le plus possible de la limite de diffraction idéale du système.

De même, la géométrie d'une lentille contribue à sa capacité à reproduire une image de bonne qualité. Le diamètre de la lentille (D), la distance focale (f) et le f/# (équation 2) affectent tous la FTM.

Le nombre f (f/#) est la capacité de collecter la lumière d'une lentille. Lorsque le diamètre de la lentille augmente, le nombre f diminue. Les lentilles à nombre f faible recueillent le plus de lumière, ce qui les rend idéales pour les applications où la lumière est restreinte. Bien qu'une valeur élevée du nombre f puisse améliorer les performances d'un objectif d'imagerie, une augmentation trop importante peut être préjudiciable car elle peut entraîner une aggravation progressive de la limite de diffraction.

Profondeur de champ (DOF)

La profondeur de champ, ou DOF, est la capacité d'un objectif à maintenir une qualité d'image souhaitée lorsque l'objet observé entre et sort de la mise au point. La distance focale est définie en fonction de la résolution et du contraste, qui diminuent lorsqu'un objet est placé plus près ou plus loin de la distance de travail optimale (Figure 5). La profondeur de champ s'applique également aux objets en profondeur, car les objectifs à DOF élevée permettent d'obtenir une image claire de l'ensemble de l'objet. La profondeur de champ est estimée par une valeur unique calculée à partir de la limite de diffraction, ce qui en fait une approximation théorique. Il est toutefois difficile d'effectuer une véritable comparaison, car de nombreux objectifs d'imagerie ne sont pas limités par la diffraction. Par exemple, deux objectifs peuvent avoir le même f/# (c'est-à-dire une limite de diffraction égale), mais n'ont pas nécessairement des performances similaires ou une profondeur de champ comparable. Par conséquent, la seule façon de déterminer réellement la profondeur de champ est d'utiliser une mire de test pour la tester.

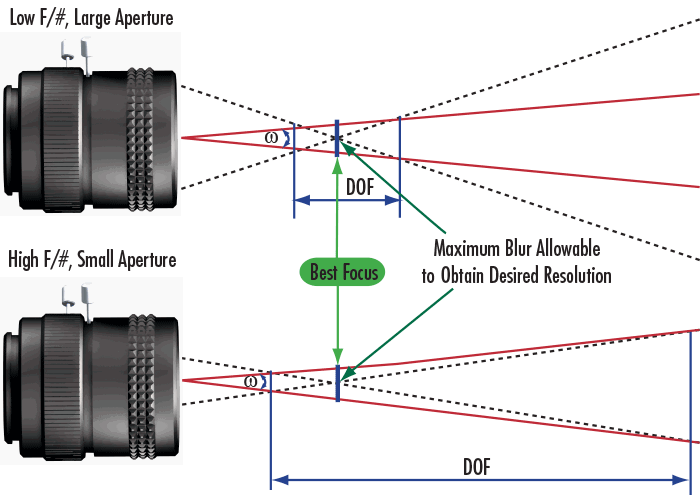
Figure 5 : Représentation géométrique de la profondeur de champ pour les objectifs à f/# faible et élevé.

Distorsion

La distorsion est un type d'aberration géométrique qui provoque une différence de grossissement de l'objet en différents points de l'image. Lorsque les rayons lumineux transportent l'image d'un objet à travers un système, plusieurs points sont mal placés par rapport au centre du champ, ou au point central de l'image. Par conséquent, la distorsion n'est pas une aberration qui provoque des flous, mais une aberration qui provoque une dislocation. La distorsion est calculée par :

où AD est la distance réelle et PD la distance paraxiale, ou distance prévue.

La distorsion, représentée par un pourcentage, peut être positive ou négative. Un pourcentage positif représente une distorsion en « coussinet », tandis qu'un pourcentage négatif représente une distorsion en « barillet ». La Figure 6 illustre la distorsion en barillet et en coussinet par rapport à une image idéale, parfaitement carrée et sans distorsion.

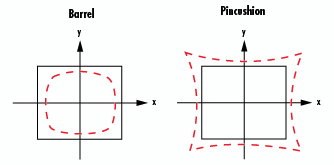
Figure 6 : Distorsion en barillet en coussinet

Bien que la distorsion soit présente dans presque tous les objectifs, elle peut être corrigée par l'utilisation de courtes distances focales. Malheureusement, les systèmes à courte focale ont tendance à souffrir davantage des effets de diffraction que leurs homologues à plus longue focale. La correction d'une composante de la qualité de l'image en affecte indéniablement une autre, ce dont il faut toujours tenir compte. Il est important de garder à l'esprit que la distorsion entraîne le déplacement, mais non la perte, d'informations sur l'objet. L'image originale, non déformée, peut être reconstruite à l'aide d'un logiciel d'analyse d'images.

TYPES DE MIRES DE TEST

Il existe une variété de mires de test pour aider à caractériser la résolution, le contraste, la fonction de transfert de modulation (FTM), la profondeur de champ (DOF) et la distorsion dans un système d'imagerie. Le guide suivant des mires les plus populaires facilite le choix de la bonne mire de test.

Mires de Résolution USAF 1951

Constituées de barres horizontales et verticales organisées en groupes et en éléments. Chaque groupe comprend jusqu'à neuf éléments dans un éventail de douze groupes. Chaque élément est composé de trois barres horizontales et de trois barres verticales également espacées les unes des autres au sein d'un groupe et correspond à une résolution associée basée sur la largeur des barres et l'espace. Les barres verticales sont utilisées pour calculer la résolution horizontale, et les barres horizontales sont utilisées pour calculer la résolution verticale. Ces mires sont très populaires lorsqu'il s'agit de choisir une mire pour tester la résolution. Voir le produit

Applications typiques

Test de résolution dans des applications telles que les équipements de test optique, les microscopes, les objectifs vidéo à fort grossissement, la microscopie à fluorescence et la microscopie confocale, la photolithographie et la nanotechnologie.

Mires de Résolution IEEE

Conçues pour caractériser la quantité de résolution qu'une caméra ou un système d'affichage est capable de reproduire à partir d'une image originale. Comme la résolution peut être différente à travers le champ de vision, la résolution horizontale et verticale peuvent être mesurées au centre de la mire ainsi qu'aux quatre coins. Les mires de résolution IEEE peuvent également être utilisées pour vérifier le balayage, la linéarité, l'aspect, l'ombrage et l'entrelacement, ainsi que pour mesurer les lignes de TV. Voir produit

Applications typiques

Test des systèmes d'imagerie analogiques

Réseaux de Ronchi

Il s'agit d'une optique à ondes carrées avec des motifs constants de barres et d'espaces qui présentent un rapport de contraste élevé. Ces réseaux sont idéaux pour les besoins d'étalonnage du réticule et du champ, et sont souvent utilisés pour évaluer la résolution, la distorsion du champ et la stabilité parfocale. Les réseaux de Ronchi ne sont pas limités au seul calcul de la résolution ; ils peuvent être utilisés pour les tests de diffraction. Voir produit

Applications typiques

Test des paramètres de résolution et de contraste, test de diffraction

Mires de Distorsion

Utilisées pour calibrer les systèmes d'imagerie pour la distorsion, qui est une aberration géométrique qui peut déplacer certaines parties de l'image. Ces mires sont constituées d'une grille de points séparés par des distances variables en fonction de l'application.

Applications typiques

Objectifs à faible distance focale, systèmes offrant un large champ de vision

Mires de Profondeur de Champ

Ces mires testent directement la profondeur de champ dans les systèmes d'imagerie sans avoir recours à des calculs. La mire doit être montée à 45° de la face de l'objectif qui est parallèle à l'objet à observer ; l'échelle de la mire est constituée de lignes horizontales et verticales qui mesurent la fréquence en paires de lignes par mm (lp/mm). Voir le produit

Applications typiques

Inspection des circuits imprimés, caméras de sécurité

Mires Étoilées

Idéales pour identifier les erreurs de mise au point, l'astigmatisme, ainsi que d'autres aberrations liées à la mise au point. La mire consiste en un cercle formé de lignes radiales noires et blanches en alternance émanant d'un point central. Parce que les lignes se rétrécissent, on a un changement continu de résolution qui peut être mesuré à la fois dans les directions verticales et horizontales sans repositionnement. Voir produit

Applications typiques

Alignement d'un système, aide à l'assemblage, comparaison de systèmes d'imagerie à résolution ou grossissement élevés

Mires de Niveaux de Gris EIA

Utiles pour tester les systèmes d'inspection optique et vidéo, ces mires consistent en un modèle standard et comportent deux échelles, l'une linéaire et l'autre logarithmique, ce qui est utile en fonction de la linéarité du détecteur utilisé. Chaque gamme comporte neuf pas qui sont accordés avec précision pour un motif en demi-teinte précis. Voir le produit

Applications typiques

Systèmes d'inspection optique et vidéo, évaluation des niveaux de contraste des caméras

Vérificateurs de Couleur

Utilisés pour déterminer la véritable balance des couleurs ou la densité optique de tout système de rendu des couleurs. Ils peuvent être étendus pour inclure plus de carrés avec un assortiment différent de couleurs et servent de référence pour tester et normaliser les systèmes d'inspection et d'analyse des couleurs. Voir produit

Applications typiques

Systèmes de rendu des couleurs, caméras numériques et photographie

Explorez les Mires de Résolution USAF 1951

Les Mires de Résolution USAF 1951 ont été et sont actuellement la référence lorsqu'il s'agit de tester la résolution d'un système d'imagerie. Elles sont constituées de barres horizontales et verticales organisées en groupes et en éléments. Chaque groupe est composé de six éléments, et chaque élément est composé de trois barres horizontales et de trois barres verticales espacées régulièrement les unes des autres. Il peut y avoir un total de douze groupes, les plus grands nombres étant utilisés pour une résolution plus élevée. Par exemple, une mire de résolution standard 1951 se compose de numéros de groupe allant de -2 à 7, tandis qu'une haute résolution va de -2 à 9 ; le numéro de l'élément est le même. La résolution est basée sur la largeur et l'espace des barres, la longueur des barres étant égale à cinq fois la largeur d'une barre (Figure 7). Une paire de lignes (lp) équivaut à une barre noire et une barre blanche. Les barres verticales sont utilisées pour calculer la résolution horizontale, et les barres horizontales sont utilisées pour calculer la résolution verticale.

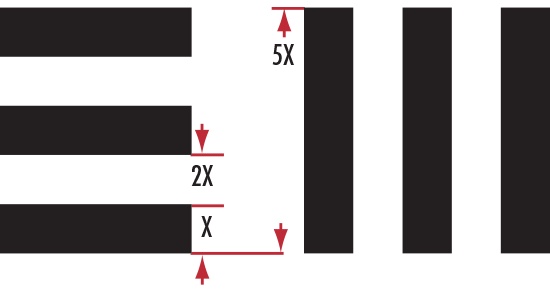
Figure 7 : Spécifications des Mire USAF 1951

Qualitativement, la résolution d'un système d'imagerie est définie comme la combinaison de groupes et d'éléments qui se trouve juste avant que les barres noires et blanches ne commencent à s'estomper. Sur le plan quantitatif, la résolution (en termes de paires de lignes par millimètre, ou lp/mm) peut être calculée comme suit :

Il est important de garder à l'esprit que le calcul de la résolution avec une mire USAF 1951 est subjectif. En d'autres termes, cela dépend de la personne qui regarde la mire. Une personne ayant une vision de 20/20 (selon le rapport de Snellen) est capable de discerner une résolution plus élevée qu'une personne ayant, par exemple, une vision de 20/25 ou 20/30. Même si le test réel donne des valeurs de résolution précises, la vision de l'utilisateur peut conduire à des mesures imprécises.

Exemples d'applications

Exemple 1 : Calcul de la résolution avec une mire de résolution USAF 1951

Lorsque l'on dispose d'un groupe et d'un nombre d'éléments spécifiés, on peut facilement calculer la résolution en lp/mm à l'aide de l'équation 4. Par exemple, si les barres verticales ou horizontales commencent à s'estomper au niveau de l'élément 3 du groupe 4, la résolution du système peut être désignée comme étant l'élément 2 du groupe 4. Pour calculer rapidement la résolution, utilisez notre Calculateur de résolution USAF 1951.

Pour convertir les lp/mm en μm, il suffit de prendre la réciproque de la valeur de résolution lp/mm et de la multiplier par 1000.

Exemple 2 : Comprendre le nombre f

Pour comprendre la relation entre le nombre f, la profondeur de champ et la résolution, prenons l'exemple d'un objectif d’imagerie de 35 mm double Gauss (Figure 8). Dans cet exemple, l'objectif sera intégré dans un système qui nécessite une résolution d'objet d'au moins 5 lp/mm (200 μm) à un contraste de 20%. La limite de diffraction ξ_c, ou fréquence de coupure, est déterminée par l'équation 7 :

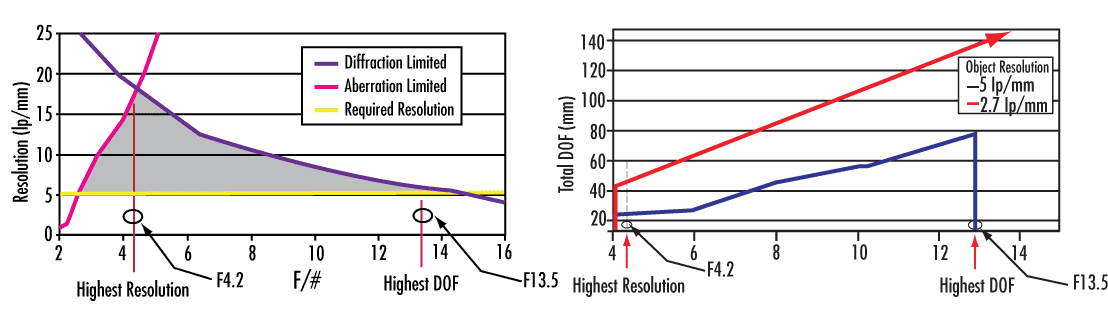
Figure 8 : Représentation graphique de la résolution en fonction du nombre f (à gauche) et de la distance focale en fonction du nombre f (à droite) pour un objectif d'imagerie double Gauss de 35 mm

où λ est la longueur d'onde du système. Pour simplifier, l'équation 7 suppose un système idéal non aberrant. Cependant, comme ce système devrait présenter des aberrations, la limite de diffraction diminue avec l'augmentation du nombre f. La détermination d'un nombre f idéal pour ce système conduit à calculer la plus grande profondeur de champ possible. En comparant la résolution au nombre f, il est évident qu'en dessous de f/3, l'objectif est limité par les aberrations et ne peut obtenir la résolution minimale souhaitée. Cependant, le fait de fermer le diaphragme permet de réduire les aberrations et d'améliorer le champ visuel. À un nombre f/4,2, les effets de diffraction causés par les éléments optiques de l'objectif d'imagerie deviennent plus importants que les effets des aberrations ; c'est à ce moment-là que l'objectif devient limité par la diffraction. Au-delà de f/4,2, la fermeture du diaphragme augmente la profondeur de champ, mais réduit la résolution. À f/13,5, la limite de diffraction définit l'étendue de la résolution souhaitée. Au-delà de f/13,5, la résolution continue de diminuer alors que la profondeur de champ continue d'augmenter. Dans cet exemple particulier, f/13,5 est le nombre f idéal pour une profondeur de champ optimale avec une résolution minimale.