Introduction à la fonction de transfert de modulation

Composants | Compréhension | Importance | Caractérisation

Lorsque les concepteurs optiques tentent de comparer les performances des systèmes optiques, une mesure couramment utilisée est la fonction de transfert de modulation (FTM). La FTM est utilisée aussi bien pour les composants simples tels qu’une qu’une lentille singulet sphérique que pour les composants complexes tels qu’un assemblage d’objectif d’imagerie télécentrique multiélément. Afin de comprendre l’importance de la FTM, veuillez prendre en considération certains principes généraux et exemples pratiques permettant de définir la FTM, notamment ses composants, son importance et sa caractérisation.

LES COMPOSANTS DE LA FTM

Pour définir correctement la fonction de transfert de modulation, il est nécessaire de commencer par définir deux termes permettant de caractériser précisément les performances d’image : la résolution et le contraste.

Résolution

La résolution représente la capacité du système d’imagerie à distinguer les détails d’un objet. Elle est souvent exprimée en paires de lignes par millimètre (où une paire de lignes est une séquence d’une ligne noire et d’une ligne blanche). Cette mesure de paires de lignes par millimètre $ \small{\left( \tfrac{\text{pl}}{\text{mm}} \right)} $ est également appelée fréquence. L’inverse de la fréquence produit l’espacement en millimètres entre les deux lignes résolues. Les mires de barres comportant une série de barres noires et blanches alternées, également espacées (par exemple, une mire USAF 1951 ou un test de Ronchi) sont parfaites pour tester les performances système. Pour des explications plus détaillées sur les mires test, consultez Choisir la mire test appropriée. Pour tous les composants optiques d’imagerie, lors de l’imagerie d’un tel modèle, les bords de lignes parfaites deviennent flous à un certain degré (Figure 1). Les images haute résolution sont celles qui montrent un grand nombre de détails résultant d’un flou minimal. Inversement, les images basse résolution manquent de détails fins.

Figure 1 : Bords de lignes parfaites avant (gauche) et après (droite) traversant un objectif d’imagerie basse résolution

Une manière pratique de comprendre les paires de lignes consiste à les considérer comme des pixels sur un capteur de caméra, où une seule paire de lignes correspond à deux pixels (Figure 2). Deux pixels de capteur de caméra sont nécessaires pour chaque paire de lignes de résolution : un pixel est dédié à la ligne rouge et l’autre à l’espace blanc entre les pixels. À l’aide de la métaphore précédemment citée, la résolution d’image de la caméra peut désormais être spécifiée comme égale à deux fois sa taille en pixel.

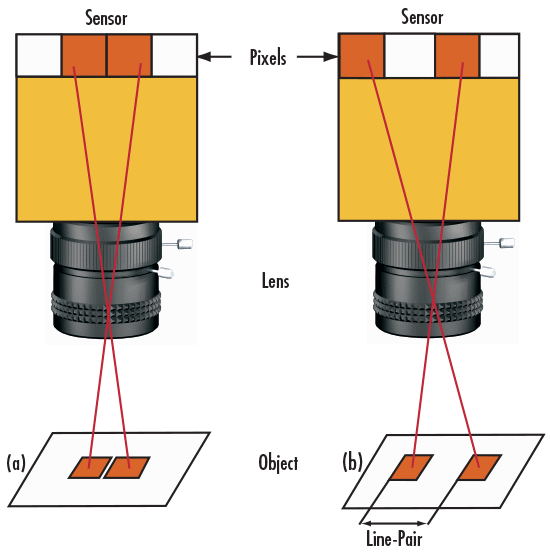
Figure 2 : Scénarios d’imagerie où (a) la paire de lignes n’est PAS résolue et (b) la paire de lignes est résolue

Proportionnellement, la résolution de l’objet est calculée à l’aide la résolution de la caméra et du grossissement primaire (PMAG) de l’objectif d’imagerie équations 1 à 2). Il est important de noter que ces équations supposent que l’objectif d’imagerie n’entraîne pas de perte de résolution.

Contraste/Modulation

Considérez la normalisation de l’intensité d’une mire de barres en attribuant une valeur maximale aux barres blanches et une valeur de zéro aux barres noires. Le traçage de ces valeurs génère une onde carrée, à partir de laquelle la notion de contraste peut être plus facilement observée (Figure 3). Mathématiquement, le contraste est calculé avec l’équation 3 :

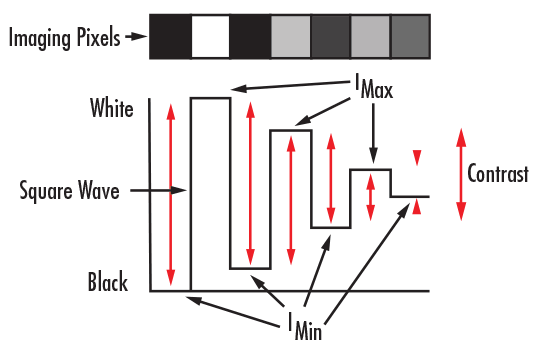
Figure 3 : Contraste exprimé en onde carrée

Lorsque ce même principe est appliqué à l’exemple d’imagerie dans la Figure 1, le diagramme d’intensité avant et après l’imagerie peut être observé (Figure 4). Le contraste ou la modulation peuvent alors être définis comme le degré de fidélité avec lequel les valeurs d’intensité minimale et maximale sont transférées du plan d’objet au plan d’image.

Pour comprendre la relation entre le contraste et la qualité de l’image, considérez un objectif d’imagerie avec la même résolution que celle utilisée dans la Figure 1 et dans la Figure 4, mais utilisée pour visionner un objet avec une fréquence de paire de lignes supérieure. La Figure 5 montre que lorsque la fréquence spatiale des lignes augmente, le contraste de l’image diminue. Cet effet est toujours présent lors du travail avec des objectifs d’imagerie de la même résolution. Pour que l’image apparaisse définie, le noir doit être réellement noir et le blanc réellement blanc, avec une quantité minimale d’échelle de gris entre les deux.

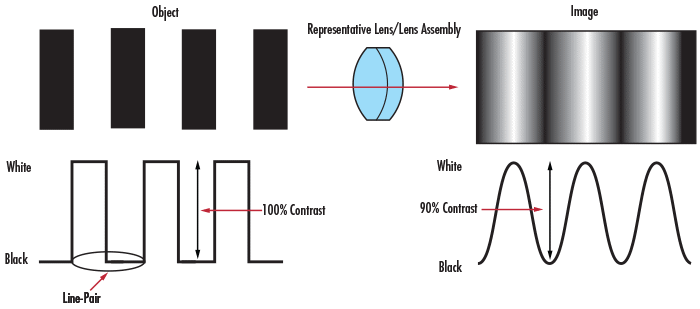
Figure 4 : Contraste d’une mire de barres et son image

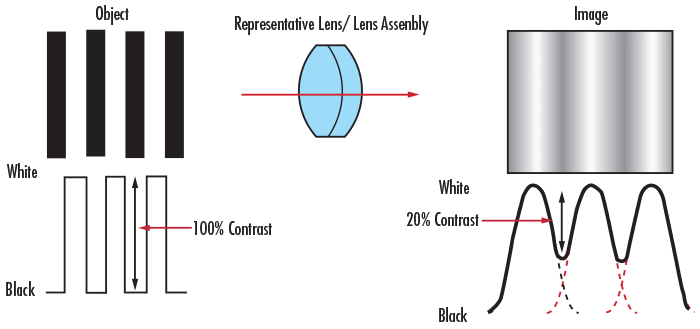
Figure 5 : Comparaison du contraste au niveau des plans d’objet et des plans d’image

Dans les applications d’imagerie, le capteur de caméra, l'objectif d’imagerie et l'illumination jouent un rôle majeur pour déterminer le contraste d’image résultant. Le contraste de l’objectif est généralement défini en termes de pourcentage du contraste de l’objet qui est reproduit. La capacité du détecteur à reproduire le contraste est généralement spécifiée en termes de décibels (dB) dans les caméras analogiques et en bits dans les caméras numériques.

COMPRENDRE LA FTM

Maintenant que les composants de la fonction de transfert de modulation (FTM), la résolution et le contraste/la modulation sont définis, penchons-nous sur la FTM à proprement parler. La FTM d’un objectif, comme son nom l’indique, est une mesure de sa capacité à transférer le contraste à une résolution particulière de l’objet à l’image. En d’autres termes, la FTM est une manière d’incorporer la résolution et le contraste dans une seule spécification. Tandis que l’espacement des lignes diminue (c’est-à-dire que la fréquence augmente) sur la mire test, il devient de plus en plus difficile pour l’objectif de transférer efficacement cette diminution du contraste ; il en résulte une diminution de la FTM (Figure 6).

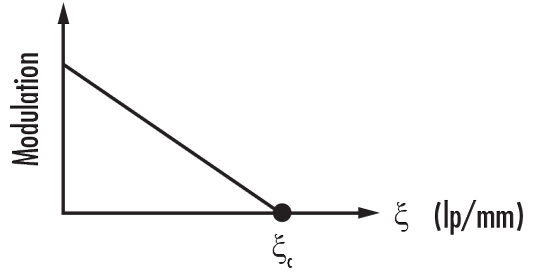
Figure 6 : FTM pour un objectif sans aberration avec une ouverture rectangulaire

Pour une image sans aberration avec une pupille circulaire, la FTM est donnée par l’équation 4, où la FTM est une fonction de la résolution spatiale $ \small{\left( \xi \right)} $, qui se réfère à la paire de lignes la plus petite que le système peut résoudre. La fréquence de coupure $ \small{\left( \xi _c \right)} $ est donnée par l’équation 6.

La Figure 6 trace la FTM d’une image sans aberration avec une pupille rectangulaire. Comme prévu, la FTM diminue tandis que la résolution spatiale augmente. Il est important de noter que ces cas sont idéalisés et qu’aucun système réel n’est complètement dénué d’aberration.

Produits pertinents

Mires de Test

Mires de Résolution USAF 1951 sur Verre

Objectifs d’Imagerie

Caméras

L’IMPORTANCE DE LA FTM

Dans l’intégration système traditionnelle (et les applications moins critiques), les performances du système sont approximativement estimées à l’aide du principe du maillon faible. Le principe du maillon faible propose que la résolution d’un système soit exclusivement limitée par le composant présentant la résolution la plus faible. Même si cette approche est très utile pour les estimations rapides, elle est imparfaite car chaque composant inclus dans le système contribue aux erreurs de l’image, produisant une image d’une qualité inférieure au maillon faible seul.

Chaque composant inclus dans un système dispose d’une fonction de transfert de modulation (FTM) associée et, par conséquent, contribue à la FTM générale du système. Cela inclut le capteur de caméra, l'objectif d’imagerie, les circuits de capture d’image, et les câbles vidéo, par exemple. La FTM résultant du système est le produit de toutes les courbes FTM de ses composants (Figure 7). Par exemple, un objectif à distance focale fixe de 25 mm et un objectif double Gauss de 25 mm peuvent être comparés en évaluant les performances système résultantes des deux objectifs avec une caméra monochrome Sony. En analysant la courbe FTM du système, il est simple de déterminer quelle combinaison produira les performances suffisantes. Dans certaines applications de métrologie, par exemple, un certain volume de contraste est requis pour une détection précise des bords de l’image. Si le contraste minimum doit être de 35% et que la résolution de l’image requise est de $ \small{30 \tfrac{\text{pl}}{\text{mm}}} $, alors l’objectif double Gauss est le meilleur choix.

La FTM est l’un des meilleurs outils disponibles pour quantifier les performances générales d’imagerie d’un système en termes de résolution et de contraste. Par conséquent, la connaissance des courbes de chaque objectif d’imagerie et capteur de caméra inclus dans le système, permet au concepteur d’effectuer la sélection appropriée lors de l’optimisation pour une résolution particulière.

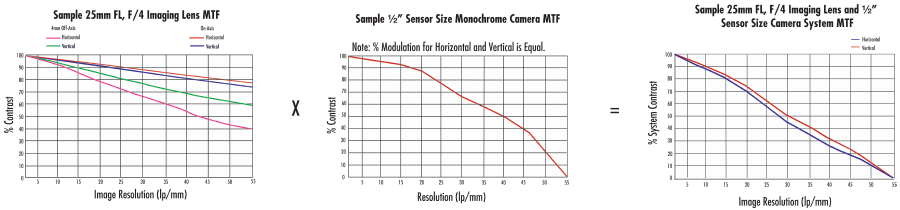
Figure 7 : La FTM du système est le produit de la FTM du composant individuel : FTM objectif × FTM caméra = FTM système

CARACTÉRISATION DE LA FTM

Détermination de la FTM réelle

Une courbe de fonction de transfert modulaire (FTM) peut être générée à partir des données optiques de n’importe quel objectif. Bien que cela puisse être utile, cela n’indique pas les performances réelles de l’objectif après avoir tenu compte des tolérances de fabrication. Les tolérances de fabrication introduisent toujours des pertes de performance au niveau de la conception optique d’origine car des facteurs tels que la géométrie et le traitement diffèrent légèrement de la lentille ou du système de lentilles idéaux. Pour cette raison, sur ses sites de fabrication, Edmund Optics® investit dans des tests et des équipements de mesure optiques pour quantifier la FTM. Ces tests et équipements de mesure de la FTM permettent la caractérisation des performances réelles des objectifs conçus et des objectifs commerciaux (dont les données optiques ne sont pas accessibles au public). Par conséquent, l’intégration précise, autrefois limitée aux objectifs avec des données connues, peut désormais inclure des objectifs commerciaux.

Lecture des graphiques/données FTM

Une zone plus importante sous la courbe FTM n’indique pas toujours un choix optimal. Un concepteur doit décider en fonction de la résolution de l’application utilisée. Comme précédemment expliqué, un graphique FTM trace le pourcentage de contraste transféré par rapport à la fréquence (cycles/mm) des lignes. Quelques éléments doivent être pris en compte concernant les courbes FTM fournies par Edmund Optics^® :

1. Chaque courbe FTM est calculée pour un point unique dans l’espace. Les points de champ typiques incluent : sur l’axe, champ à 70% et plein champ. 70% est un point de référence courant car il capture environ 50% de la zone d’imagerie totale.
2. Les données FTM hors axe sont calculées dans les cas tangentiels et sagittaux (marqués T et S, respectivement). Occasionnellement, une moyenne des deux est présentée au lieu de deux courbes individuelles.
3. Les courbes FTM sont dépendantes de plusieurs facteurs, tels que les conjugués, les gammes d’ondes et les f/N du système. Une courbe FTM est calculée à des valeurs spécifiées pour chaque facteur ; par conséquent, il est important d’examiner ces facteurs avant de déterminer si un composant fonctionnera pour une application donnée.
4. La fréquence spatiale est exprimée en termes de cycles (ou paires de lignes) par millimètre. L’inverse de cette fréquence produit l’espacement d’une paire de lignes (un cycle d’une barre noire et d’une barre blanche) en millimètres.
5. 5. La courbe FTM nominale est produite à l’aide des données optiques standard disponibles dans les programmes de conception optique. Ces données figurent également sur notre site mondial, dans nos catalogues imprimés et dans nos catalogues d’objectifs et de lentilles fournis à Zemax^®. La FTM nominale représente le meilleur scénario et ne prend pas en compte les tolérances de fabrication.

Sur le plan conceptuel, la FTM peut être difficile à saisir. Pour comprendre la notion de transfert de contraste d’un plan d’objet à un plan d’image, le mieux est peut-être d’examiner un exemple réel. Les Figures 8 à 12 comparent les courbes FTM et les images pour deux objectifs à distance focale fixesde 25 mm : Objectif Micro-Vidéo Conjugué Fini #54-855 et Objectif Compact à Distance Focale Fix #59-871. La Figure 8 montre une FTM à diffraction polychromatique pour ces deux objectifs. Selon les conditions de test, les deux objectifs peuvent générer des performances équivalentes. Dans cet exemple donné, les deux tentent de résoudre le groupe 2, éléments 5 à 6 (indiqués par les encadrés rouges dans la Figure 10) et le groupe 3, éléments 5 à 6 (indiqués par les encadrés bleus dans la Figure 10) sur une mire de résolution USAF 1951 (Figure 9). En ce qui concerne la taille réelle de l’objet, le groupe 2, éléments 5 à 6 représentent 6,35 à $ \small{7,13 \tfrac{\text{pl}}{\text{mm}}} $ (14,03 à 15,75 μm) et le groupe 3, éléments 5 à 6 représentent 12,70 à $ \small{14,25 \tfrac{\text{pl}}{\text{mm}}} $ (7,02 à 7,87 μm). Pour une méthode simple de calcul des numéros de groupe et d’élément donnés de la résolution, utilisez notre outil technique EO Résolution USAF 1951.

Avec les mêmes paramètres de test, il ressort clairement que le #59-871 (avec une meilleure courbe FTM) génère de meilleures performances d’imagerie que le #54-855 (Figures 11 à 12). Dans cet exemple réel avec ces éléments USAF 1951 particuliers, une valeur de modulation supérieure à des fréquences spatiales plus élevées correspond à une image plus nette ; toutefois, ce n’est pas toujours le cas. Certains objectifs sont conçus pour être capables de résoudre très précisément les fréquences spatiales inférieures et présentent une fréquence de coupure très faible (c’est-à-dire qu’ils ne peuvent résoudre de fréquences spatiales plus élevées). Si la mire avait été du groupe 1, éléments 5 à 6, les deux objectifs auraient généré davantage d’images similaires étant donné leurs valeurs de modulation à des fréquences plus faibles.

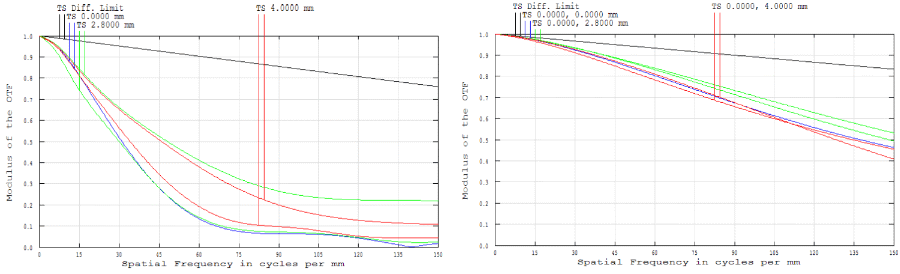
Figure 8 : Comparaison de la FTM à diffraction polychromatique pour l’Objectif Micro-Vidéo Conjugué Fini (à gauche) #54-855 et l’Objectif Compact à Distance Focale Fixe (à droite) #59-871

Figure 9 : 1951 Mire de résolution USAF 1951

Figure 10 : Comparaison de l’Objectif Micro-Vidéo Conjugué Fini (à gauche) #54-855 et de l’Objectif Compact à Distance Focale Fixe (à droite) #59-871, groupe de résolution 2, éléments 5 à 6 (encadrés rouges) et groupe 3, éléments 5 à 6 (encadrés bleus) sur une mire de résolution USAF 1951

Figure 11 : Comparaison de l’Objectif Micro-Vidéo Conjugué Fini (à gauche) #54-855 Finite Conjugate Micro-Video Lens (Left) and #59-871 groupe de résolution 2, éléments 5 à 6 sur une mire de résolution USAF 1951

Figure 12 : Comparaison de l’Objectif Micro-Vidéo Conjugué Fini (à gauche) #54-855 Comparaison de l’Objectif Micro-Vidéo Conjugué Fini (à gauche) #59-871, groupe de résolution 3, éléments 5 à 6 sur une mire de résolution USAF 1951

La fonction de transfert de modulation (FTM) est l’un des paramètres les plus importants pour la mesure de la qualité de l’image. Les concepteurs et ingénieurs se rapportent fréquemment aux données de FTM, notamment dans les applications où le succès ou l’échec dépend du niveau de précision d’imagerie d’un objet. Pour pleinement saisir la FTM, il est nécessaire de comprendre dans un premier temps les concepts de résolution et de contraste, ainsi que la manière dont une image d’objet est transférée d’un plan d’objet à un plan d’image. Même si cela peut sembler intimidant, la compréhension et in fine l’interprétation des données FTM représentent un outil puissant pour un concepteur optique. Combinée aux connaissances et à l’expérience, la FTM peut considérablement faciliter le choix de l’objectif approprié, malgré la multitude d’offres.

Références

1. Dereniak, Eustace. "OPTI 340 - Optical Design." Lecture, The University of Arizona, Tucson, AZ, Spring 2010.
2. Geary, Joseph M. "Chapter 34 – MTF: Image Quality V." In Introduction to Lens Design: With Practical Zemax Examples, 389-96. Richmond, VA: Willmann-Bell, 2002.
3. Hecht, Eugene. "11.3.5 Transfer Functions." In Optics, 550-56. 4th ed. San Francisco, CA: Addison-Wesley, 2001.
4. Smith, Warren J. "Chapter 15.8 The Modulation Transfer Function." In Modern Optical Engineering, 385-90. 4th ed. New York, NY: McGraw-Hill Education, 2008.