Comprendre la rugosité de surface

Auteurs : Victoria Marcune,Shawn Iles

La rugosité d'une surface est l'un des éléments décrivant la façon dont la forme d'une surface s'écarte de sa forme idéale, les valeurs élevées correspondant à des surfaces plus rugueuses tandis que les valeurs faibles indiquent que la surface est lisse. La rugosité décrit des erreurs à haute fréquence spatiale, c'est-à-dire de très petites déviations de l'ordre de l'angström (10^-10 m). Il est essentiel de comprendre la rugosité des surfaces optiques pour contrôler la diffusion de la lumière, car la diffusion peut être proportionnelle à la rugosité de la surface de l'optique. La diffusion et l'absorption de la lumière par la rugosité de la surface ont un impact significatif sur les applications telles que les systèmes laser de haute puissance, qui peuvent avoir une incidence négative sur l'efficacité et le seuil de dommage laser. En plus d'avoir un impact sur le seuil de dommage, le rayonnement laser de forte puissance diffusé peut constituer un risque pour la sécurité de toute personne se trouvant à proximité du système, car la lumière est redirigée dans des directions non souhaitées. La norme actuellement utilisée pour la rugosité de surface est la norme ISO 10110-8, qui définit la manière dont la rugosité de surface doit être analysée et spécifiée.

Lire les informations sur la rugosité de la surface

Un dessin conforme à la norme ISO 10110-8 énumère les spécifications suivantes pour donner une description complète de la surface optique.

Figure 1 : Exemple de spécification de la rugosité de surface

Finition de la surface, montrée dans la Figure 1 comme « P3 » :

Cette variable indique l'état de surface. Pour les spécifications de polissage simples, il peut s'agir d'un G, pour surface rectifiée (G = ground), ou d'un P pour indiquer qu'il s'agit d'un polissage optique. Le degré de polissage sera attribué de 1 à 4 en fonction du degré de lissage en termes de microdéfauts par balayage de 10 mm, comme indiqué ci-dessous dans le Tableau 1 :

Désignation du degré de polissage	Nombre, N, de microdéfauts par 10 mm de longueur d'échantillonnage
P1	80 ≤ N < 400
P2	16 ≤ N < 80
P3	3 ≤ 16
P4	N < 3

Tableau 1 : Indication du degré de lissage en termes de microdéfauts

Méthode statistique utilisée, représentée dans la Figure 1 par « Rq 4 » :

Elle indique la méthode statistique utilisée pour mesurer la rugosité de la surface, suivie de la valeur.

Largeur de bande spatiale, représentée dans la Figure 1 par « 1/0,003 » :

Ceci spécifie la largeur de bande spatiale allant de la limite supérieure à la limite inférieure.

Fréquences spatiales et groupes de fréquences

Lors de la quantification de la texture de la surface d'un composant optique, il est important de définir le niveau de résolution spatiale mesuré. La texture de la surface, ou la forme complète d'une surface, peut être divisée en trois groupes principaux de fréquences spatiales : la rugosité, l'ondulation et la figure.

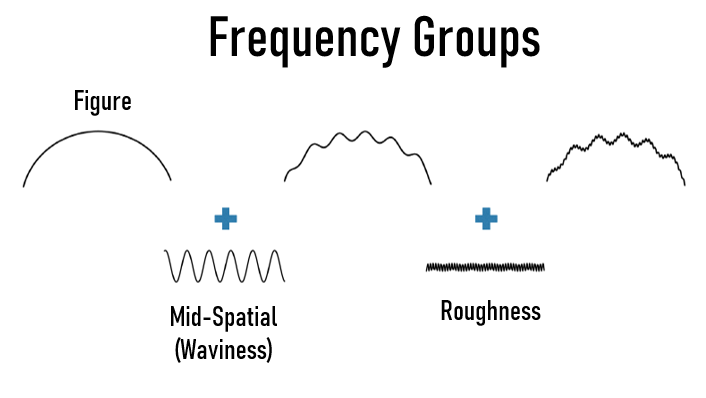
Figure 2 : La figure, l'ondulation et la rugosité caractérisent la texture de la surface à différentes échelles

La Figure 2 montre comment la figure, l'ondulation et la rugosité de surface caractérisent ensemble toutes les façons dont une surface s'écarte de sa forme idéale. La figure décrit la forme générale de la surface et constitue la plus grande échelle, ou les plus grandes fréquences spatiales, qui seront analysées. Les erreurs décrites par la figure sont de l'ordre de dixièmes de mm à cm. L'ondulation mesure les erreurs de fréquence spatiale moyenne décrivant des caractéristiques de l'ordre de µm à mm. La rugosité est la plus petite forme d'erreur et décrit des anomalies très rapprochées dans la texture de la surface, de l'ordre de dixièmes d'Angstroms à des dizaines de µm.

Paramètres de rugosité de surface selon ISO 10110-8

L'objectif de la norme ISO 10110-8 est de spécifier des règles pour définir la texture de la surface. Selon l'ISO, « La texture d’une surface est la caractéristique d'une surface qui peut être décrite efficacement à l'aide de méthodes statistiques ». La norme ISO décrit 5 méthodes statistiques utilisées pour décrire les surfaces optiquement lisses. Ces méthodes peuvent être utilisées en combinaison et sur différentes largeurs de bande spatiales. La définition des limites supérieure et inférieure de la fréquence spatiale est essentielle pour obtenir des résultats précis. Si aucune fréquence spatiale n'est définie, les normes ISO 10110-8 prévoient une plage de 0,0025 mm à 0,08 mm.

1 & 2. Rugosité et ondulation RMS : La méthode de la racine carrée moyenne (RMS) est la méthode la plus courante pour spécifier les surfaces optiquement lisses aux États-Unis, tandis qu'en Europe, il est plus courant de spécifier la rugosité absolue. La moyenne quadratique des écarts de hauteur de profil par rapport à la ligne moyenne est utilisée pour analyser statistiquement le caractère lisse d'une surface optique. La rugosité RMS, $ Rq $, fait référence au profil de rugosité tandis que l'ondulation RMS, $ Wq $, fait référence au profil d'ondulation. Les deux sont mesurés à l'aide de la même méthode RMS, mais sur des fréquences spatiales différentes.

$$ \{ Rq, Wq \} \in T $$

$$ T = \sqrt{\frac{1}{lr} \int_0^{lr} Z^2 \! \left(x \right) \text{d} x} $$

Où :

$ Rq $ : Rugosité de la surface (écart quadratique moyen)

$ Wq $ : Ondulation de la surface (écart quadratique moyen)

$ T $ : Texture de surface généralisée (rugosité ou ondulation ; écart quadratique moyen)

$ lr $ : Longueur de l'échantillon

$ Z \! \left( x \right) $ : Profil de la surface le long de l'axe x

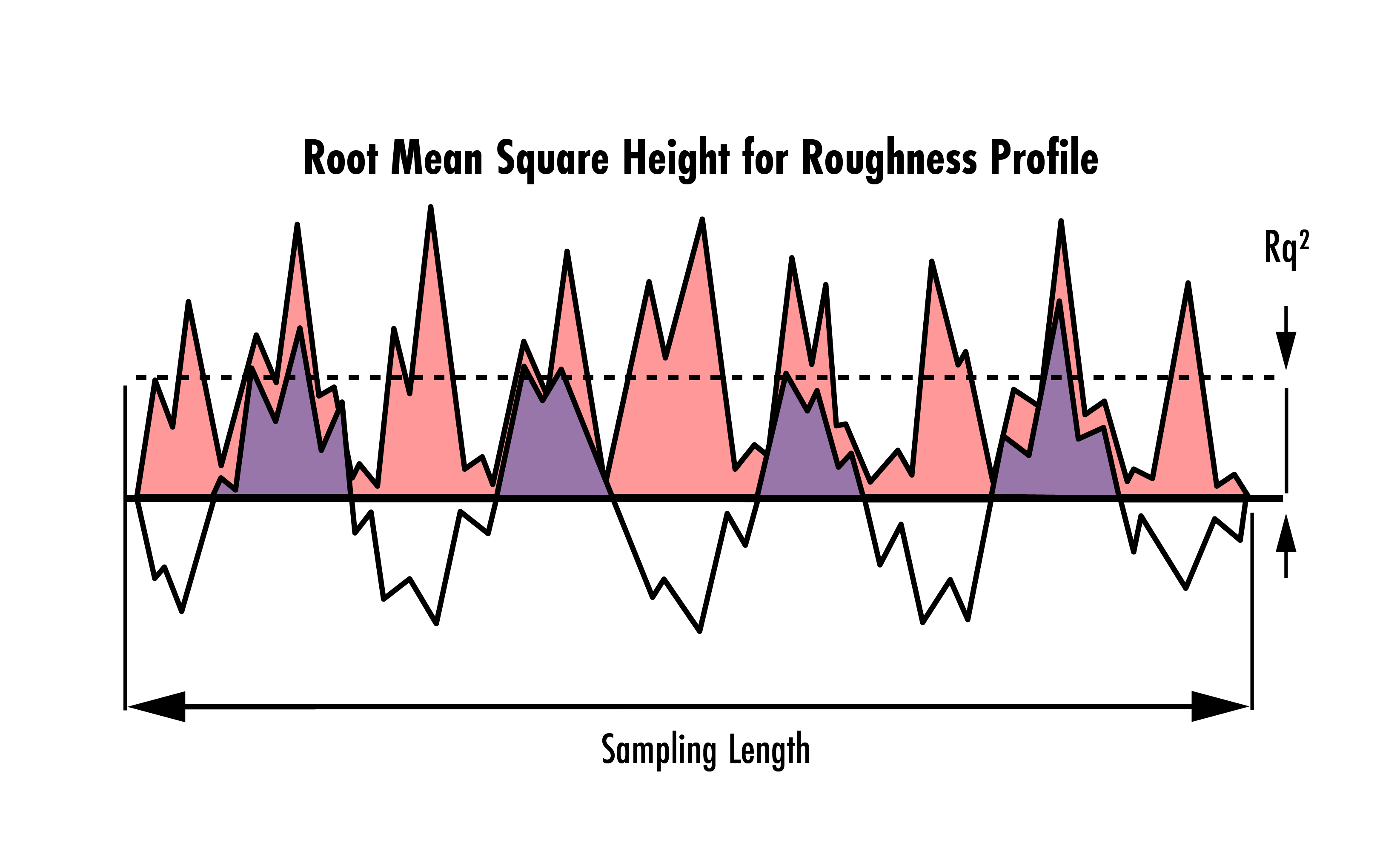
Exemple de profil de rugosité mesuré sur une longueur d'échantillonnage donnée. Rq2 indique la hauteur moyenne quadratique.

Figure 3 : Exemple de profil de rugosité mesuré sur une longueur d'échantillonnage donnée. Rq² indique la hauteur moyenne quadratique

3. Pente RMS : Comme pour la rugosité et l'ondulation RMS, les surfaces optiquement lisses peuvent être spécifiées à l'aide de la pente RMS de l'inclinaison locale, $ \tfrac{\text{d} Z \left( x \right)}{\text{d}x} $, de la surface sur une longueur d'échantillonnage donnée.

$$ \Delta T = \sqrt{ \frac{1}{lr} \int_0 ^{lr} \left[ \frac{\text{d} Z \! \left( x \right) }{\text{d} x} \right]^2 \text{d}x } $$

$$ \begin{pmatrix} T\\ T \Delta q \end{pmatrix} = \begin{Bmatrix} \begin{pmatrix} Rq\\ R \Delta q \end{pmatrix} \text { pour } 1 \large{\unicode[computer modern]{x212B}} \leq lr\leq 1 \large{\unicode[computer modern]{x03BC}} \normalsize{\text{m}} \\ \begin{pmatrix} Wq\\ W \Delta q \end{pmatrix} \text { pour } 1 \large{\unicode[computer modern]{x03BC}} \normalsize{\text{m}} < lr\leq 1 \text{mm} \end{Bmatrix} $$

$$ \Delta T = \sqrt{ \frac{1}{lr} \int_0 ^{lr} \left[ \frac{\text{d} Z \! \left( x \right) }{\text{d} x} \right]^2 \text{d}x } $$

(Faire défiler la page à droite pour voir l'équation complète)

Où :

$ R \Delta q $ : Pente de la rugosité de la surface (pente moyenne quadratique)

$ W \Delta q $ : Pente de l'ondulation de la surface (pente quadratique moyenne)

4. Donnée sur la densité des microdéfauts : Les microdéfauts sont les creux et les rayures que l'on peut trouver sur une surface optiquement lisse. Ils sont généralement quantifiés à l'aide d'un profilomètre optique, d'un microscope ou d'une loupe de mesure microscopique. La norme ISO 10110-8 stipule que « le nombre de microdéfauts, $ N $, doit être déterminé sur un balayage linéaire de 10 mm avec une résolution de 3 µm, ou sur une surface de 300 µm $ \times $ 300 µm avec la même résolution. »

5. Fonction de densité spectrale de puissance (DSP) : La fonction DSP est l'une des méthodes statistiques les plus complètes pour mesurer la rugosité de la surface. Elle permet une description complète des caractéristiques de la texture de la surface en fournissant la force relative de chaque composante de la rugosité en fonction de la fréquence spatiale.

$$ \text{PSD} \! \left( f_x, f_y \right) = \lim_{L \to \infty} \frac{1}{L^2} \left| \int_{-L/2}^{L/2} \int_{-L/2}^{L/2} z \! \left( x, y \right) \exp{ \left[ -2 \pi j \left( f_x x + f_y y \right) \right] } \text{d} x \text{d} y \right| $$

(Faire défiler la page à droite pour voir l'équation complète)

Il s'agit de l'équation générale utilisée pour calculer la DSP d'une surface bidimensionnelle. $ f_x $ et $ f_y $ sont les fréquences spatiales de la texture de la surface $ z \! \left( x, y \right) $, qui est défini sur une surface carrée de longueur de côté, $ L $.

La métrologie utilisée pour mesurer la rugosité de surface

Il existe toute une série de technologies de métrologie qui sont particulièrement adaptées aux différentes fréquences spatiales. Les plus courantes sont l'interférométrie conventionnelle, l'interférométrie à lumière blanche et la microscopie à force atomique. La Figure 4 ci-dessous montre quelles sont les régions et les longueurs d'onde les mieux adaptées à ces technologies.

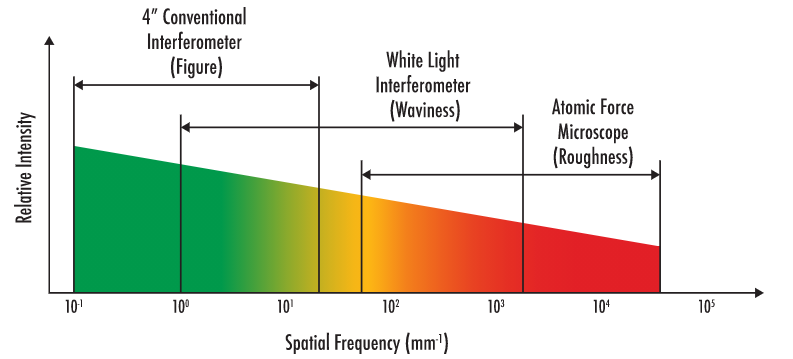
Figure 4 : Gamme de fréquences spatiales d'un équipement de métrologie typique.

L'interférométrie conventionnelle est idéale pour mesurer les erreurs à faible fréquence spatiale. Cette catégorie d'erreurs de surface est appelée erreurs de figure et est associée à des polynômes de Zernike typiques. Les polynômes de Zernike décrivent les erreurs causées par les aberrations de front d'onde lorsqu'un composant optique s'écarte d'une forme idéale. Un interféromètre à lumière blanche (WLI) est le mieux adapté pour mesurer l'ondulation ou les erreurs de la gamme de fréquences spatiales moyennes. L'ondulation est souvent attribuée à la création d'effets tels que le flou et la diminution du contraste. Enfin, le microscope à force atomique (AFM) offre la meilleure résolution pour les erreurs spatiales à haute fréquence qui caractérisent la rugosité de la surface optique. Ces groupes se chevauchent en partie, car l'interféromètre à lumière blanche et le microscope à force atomique peuvent tous deux être utilisés pour mesurer la rugosité. Le choix de l'équipement dépend en partie de la longueur d'onde de l'application. Par exemple, la WLI est idéale pour mesurer des spectres visibles ou infrarouges, car ils sont généralement analysés à des fréquences inférieures à 2 000 cycles/mm.

Spécifier la qualité de surface pour les composants optiques ultrarapides

Lors de l'analyse d'optiques ultrarapides, les fabricants doivent faire preuve de discernement pour spécifier la qualité de la surface, car il n'existe actuellement aucune norme en la matière. Plusieurs fabricants d'optiques ultrarapides ne spécifient que la qualité de la surface du pré-traitement, tandis que d'autres fabricants n'indiquent qu'une qualité de 20-10 ou plus pour le post-traitement.

Les optiques créées pour les applications ultrarapides comportent généralement des traitements épais et spécialisés qui nécessitent un long processus de pulvérisation. En raison de la longueur de ce processus, des imperfections peuvent être pulvérisées dans le traitement, ce qui donne un aspect cosmétique de « poussière » ou de qualité de surface irrégulière. Plutôt que de la poussière, ces imperfections sont créées par de petites poussées dans le flux du matériau pulvérisé. Pendant toute la durée du processus de revêtement, il peut y avoir des variations de la vitesse de pulvérisation qui entraînent des microdépôts locaux du traitement.

Aspect typique d'une optique avec un traitement ultrarapide. Malgré l'apparence d'une qualité de surface irrégulière, Edmund Optics garantit les performances spécifiées de nos optiques ultrarapides.

Figure 5 : Aspect typique d'une optique avec un traitement ultrarapide. Malgré l'apparence d'une qualité de surface irrégulière, Edmund Optics garantit les performances spécifiées de nos optiques ultrarapides.

Malgré leur apparence, ces imperfections ont des effets négligeables sur les performances globales de l'optique. En raison de la taille relativement petite de ces imperfections, les parties affectées du faisceau deviennent insignifiantes si l'on considère les propriétés du film, telles que la dispersion de retard de groupe et la réflectivité. Bien que négligeables dans la plupart des cas, les applications qui nécessitent des faisceaux de petite taille ou une perte ultra-faible peuvent souffrir d'une augmentation de la diffusion à travers le système en raison de ces imperfections. Pour répondre à des spécifications plus strictes, des mesures spéciales peuvent être prises pour réduire la diffusion globale, par exemple en commençant par un substrat superpoli.

La métrologie chez Edmund Optics^®

Mesurer ce que vous produisez est un élément clé de la fabrication. Edmund Optics utilise un programme de qualité global strict pour s'assurer que les composants répondent aux exigences spécifiées. Une gamme d'équipements comprenant des interféromètres, des profilomètres, des machines de mesure des coordonnées (CMM) et une multitude d'autres appareils de métrologie optique et mécanique sont utilisés pour réaliser des essais en interne afin de déterminer la rugosité de la surface et d'autres propriétés optiques. Pour en savoir plus sur nos capacités de métrologie personnalisée, veuillez consulter notre page web consacrée aux capacités de métrologie.

Références

ISO 10110-8:2019, Optics and photonics — Preparation of drawings for optical elements and systems — Part 8: Surface texture
Filhaber, John. “LARGE OPTICS: Mid-Spatial-Frequency Errors: The Hidden Culprit of Poor Optical Performance.” Laser Focus World, 13 Aug. 2013
“Root Mean Square Slope (Rδq, Pδq, Wδq): Surface Roughness Parameters.” Root Mean Square Slope (Rδq, Pδq, Wδq) | Surface Roughness Parameters | Introduction To Roughness | KEYENCE America
Deck, Leslie L., and Chris Evans. “High Performance Fizeau and Scanning White-Light Interferometers for Mid-Spatial Frequency Optical Testing of Free-Form Optics.” Advances in Metrology for X-Ray and EUV Optics, 2005, https://doi.org/10.1117/12.616874.
Jayson Nelson, Shawn Iles, "Creating sub angstrom surfaces on planar and spherical substrates", Proc. SPIE 11175, Optifab 2019, 1117505 (15 November 2019); https://doi.org/10.1117/12.2536689