Diagrammes de tunnel de prismes

Les prismes sont utilisés pour replier les chemins optiques, manipuler les orientations et les tailles des images, et diffracter la lumière. Dans de nombreuses applications, une combinaison de prismes est utilisée pour obtenir plusieurs de ces effets. Pour concevoir des assemblages contenant plusieurs prismes, il est important de comprendre où la lumière entre, se déplace et sort par chaque prisme, et il peut également être important de comprendre la longueur du chemin optique de la lumière lorsqu'elle traverse le prisme. Ce chemin peut être facilement modélisé à l'aide de diagrammes de tunnel de prismes.

Un diagramme de tunnel de prisme est une figure bidimensionnelle (2D) qui montre le chemin optique qu'un rayon emprunte à travers un prisme.¹ Cette technique est utilisée pour visualiser la longueur totale du chemin parcouru par les rayons à travers le prisme. Dans ce schéma, le prisme est représenté par la section transversale caractéristique, à l'échelle. Un rayon part de l'extérieur du prisme et entre par l'une des faces. À l'intérieur du prisme, le rayon entre en contact avec une autre des faces du prisme. Si le rayon frappe la nouvelle surface à un angle égal ou supérieur à l'angle critique (associé aux indices de réfraction des milieux interfaciaux), ou si cette surface est recouverte d'un traitement miroir approprié, alors la lumière sera totalement réfléchie à l`intérieur ou presque totalement à l’intérieur. Lorsque le rayon se réfléchit sur cette surface, la section transversale représentant le prisme est inversée par rapport à la ligne représentant la surface réfléchissante du prisme, de sorte que le rayon semble continuer à traverser la section transversale suivante sans changer sa direction initiale à travers la première section transversale. Si le rayon rencontre une surface sans revêtement réfléchissant à un angle qui n'est pas supérieur ou égal à l'angle critique, alors la lumière traversera cette surface et sortira du prisme. La Figure 1 présente un exemple de diagramme de tunnel pour un prisme penta, à côté d'un diagramme typique de la trajectoire du rayon.

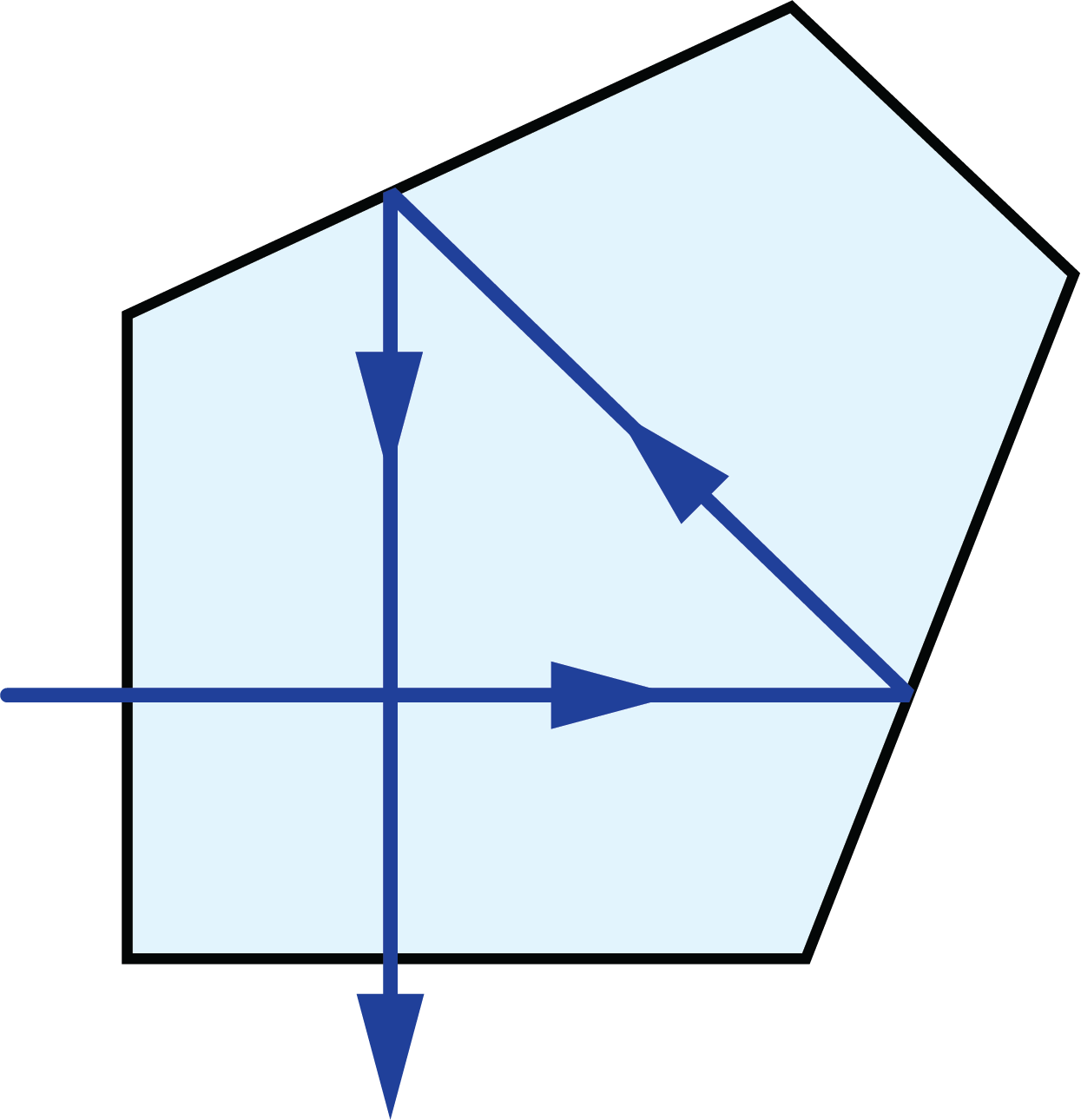
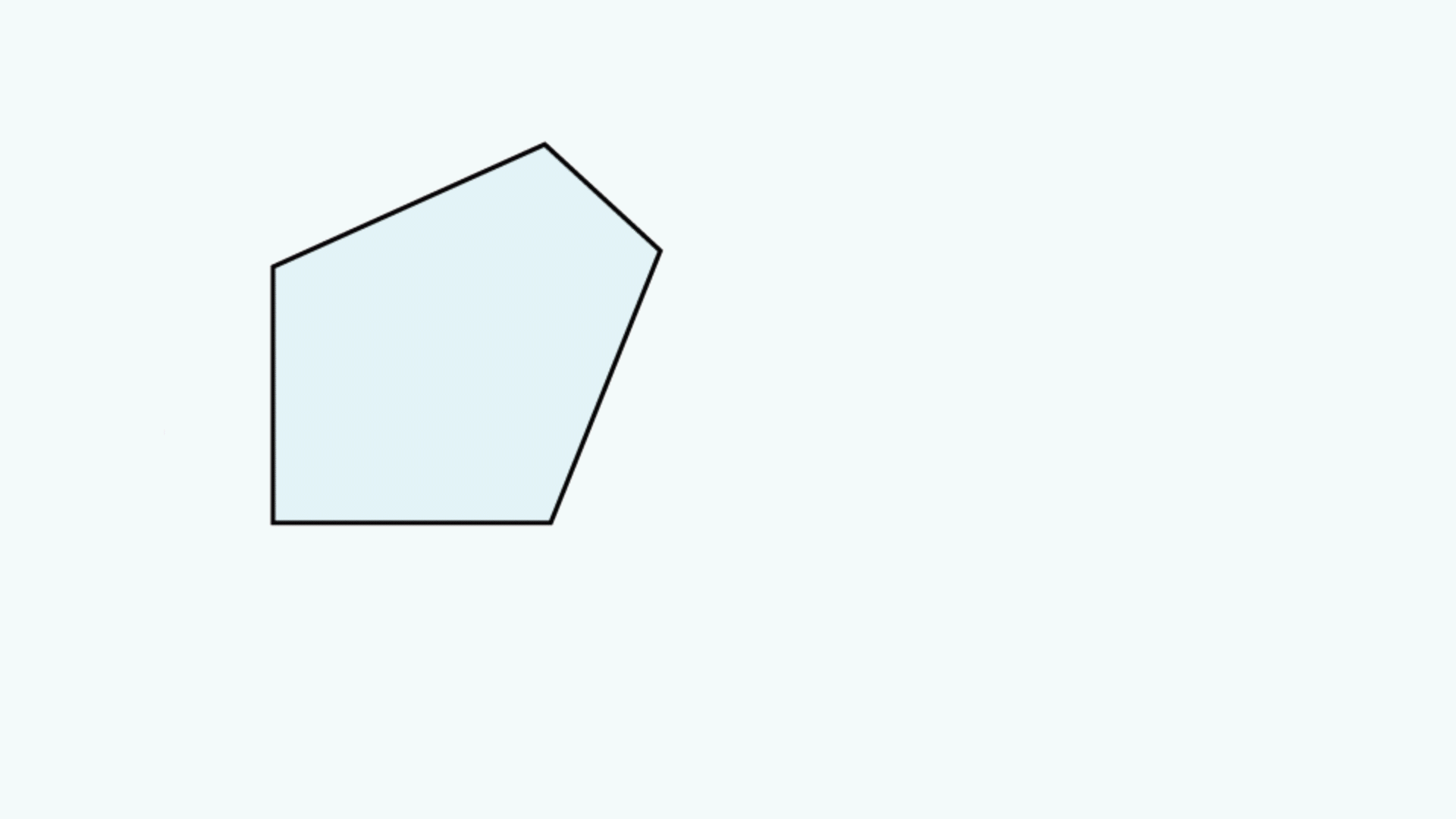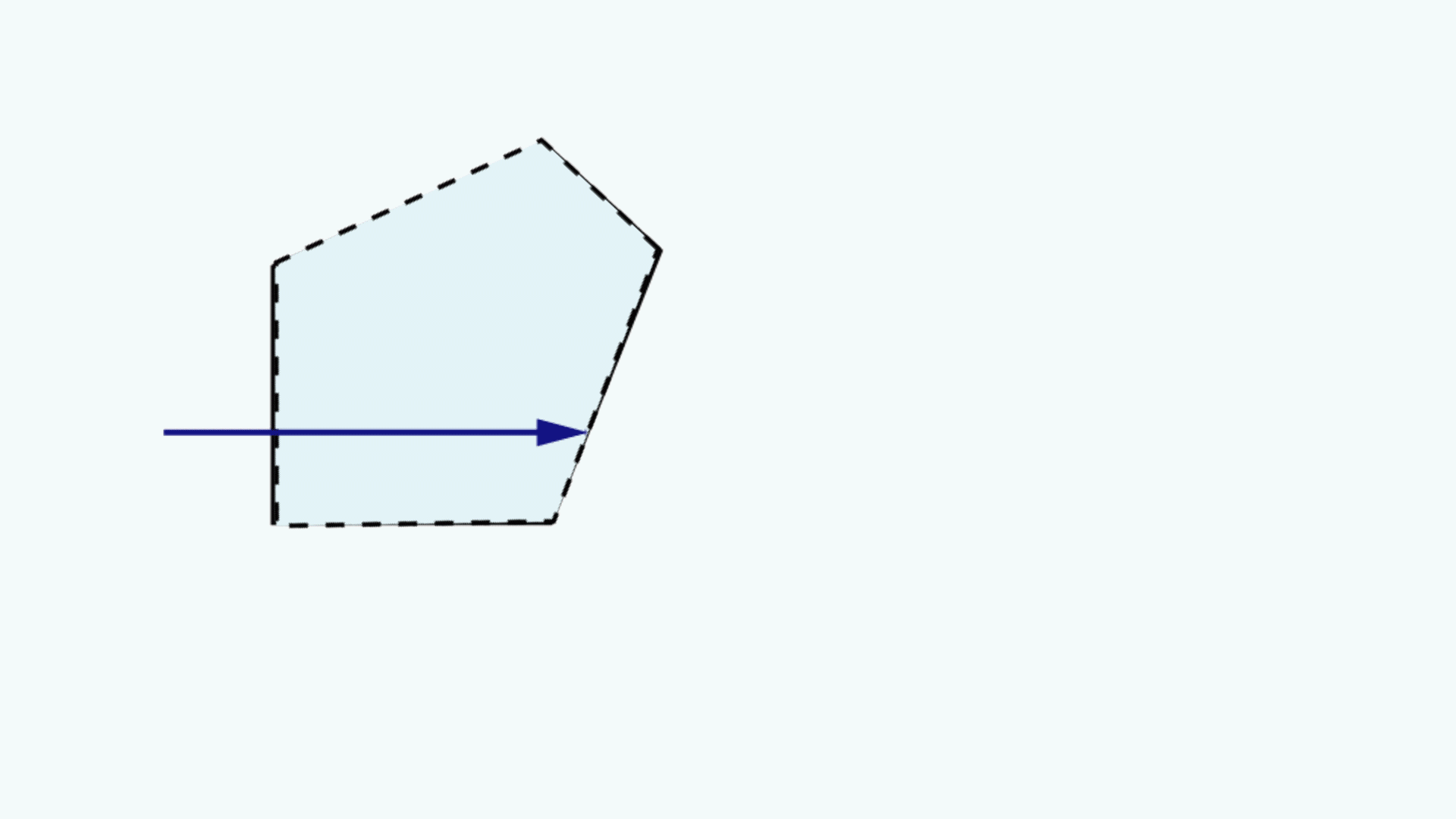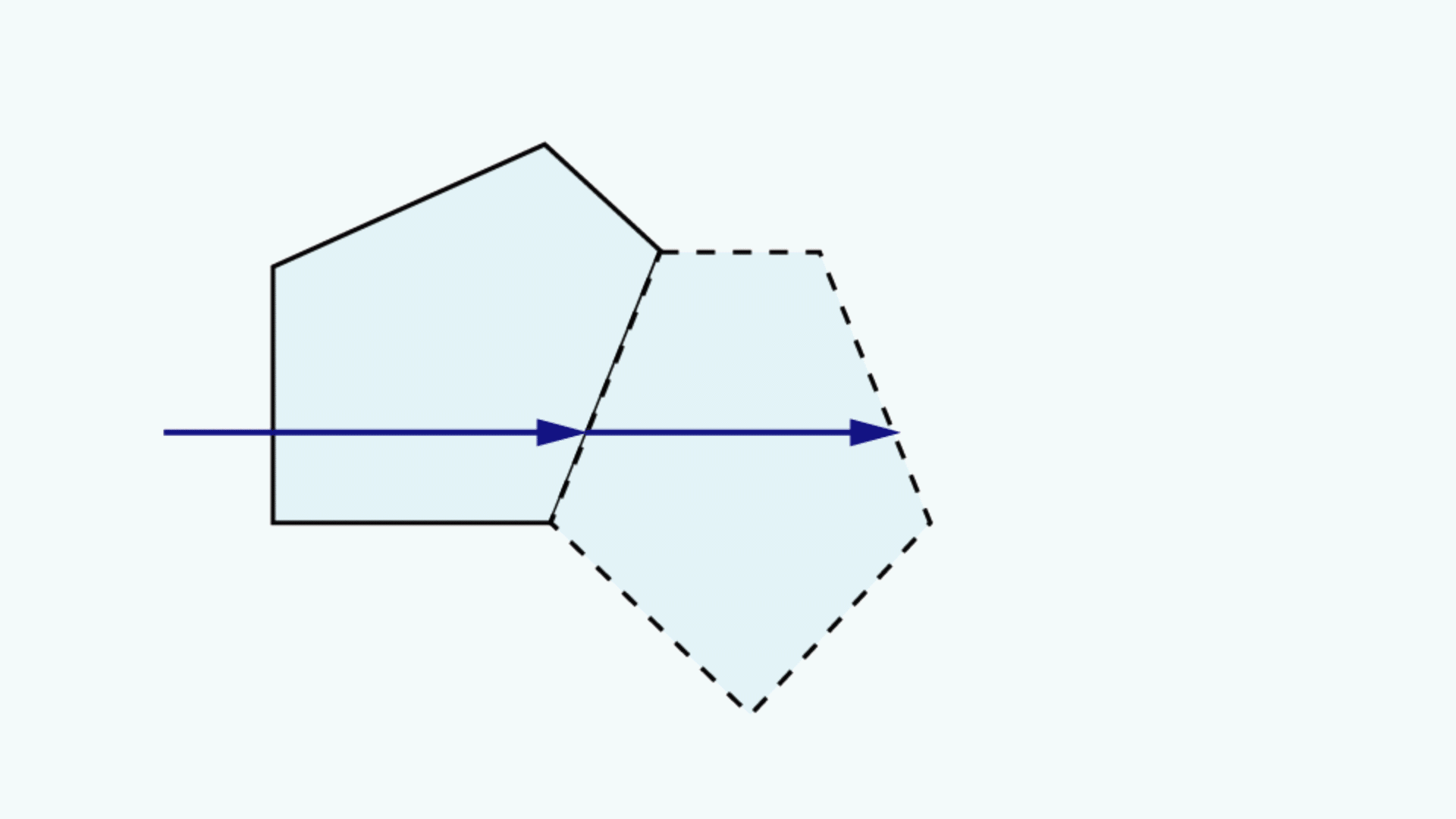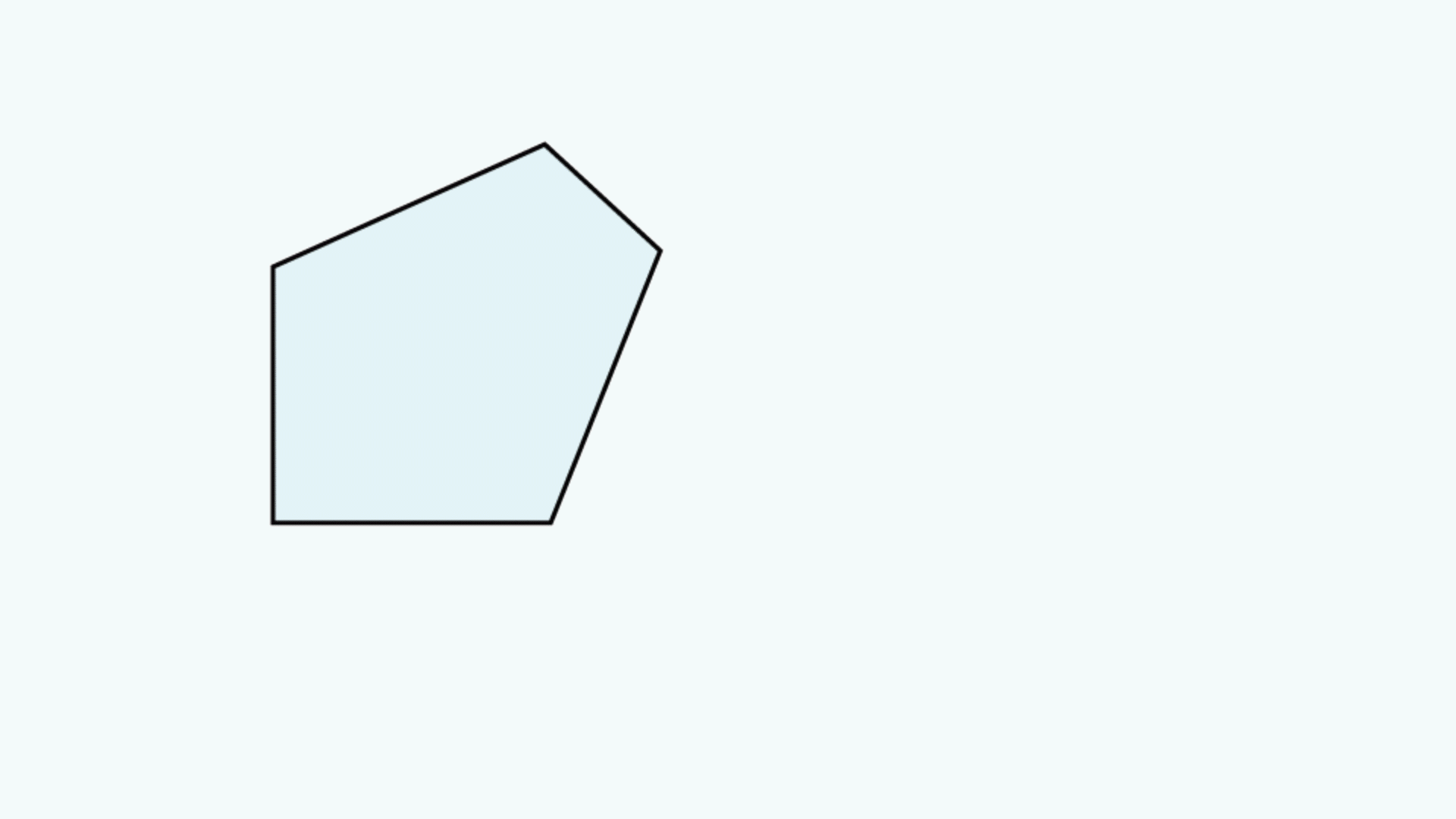
Figure 1 : En haut : Le diagramme typique du trajectoire des rayons pour un prisme penta. En bas : Le diagramme de tunnel de prismes pour ce trajectoire des rayons à travers le même prisme penta.

Un diagramme de tunnel aide à montrer l'ouverture nette d'un prisme et peut désigner l'endroit où le vignettage se produira, déterminant ainsi le champ de vision du prisme. Les prismes peuvent avoir plusieurs diagrammes de tunnel uniques pour différents chemins optiques à travers le prisme. Des diagrammes uniques peuvent être réalisés lorsque la lumière pénètre dans un prisme par une variété de faces et d'angles différents. Par exemple, les prismes Dove sont couramment utilisés dans plusieurs orientations différentes pour réaliser différents types de transformations d'images. Chacun de ces différentes trajectoires de rayons à travers le prisme a des diagrammes de tunnel différents (Tableau 1). 
 

Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant

Tableau 1 : Diagrammes communs de tunnels de prismes Dove

Dans les diagrammes du haut et du bas, la lumière entre et sort par les mêmes faces, mais les angles d'entrée et de sortie sont différents. En outre, le premier schéma ne comporte qu'une seule surface de réflexion, tandis que le deuxième et le troisième comportent respectivement deux et trois réflexions.

Dans les diagrammes des trajectoires des rayons 2D, un symbole "V" est ajouté pour indiquer un toit, ou une section où deux faces du prisme se rencontrent à un angle de 90° et pour une forme « en toit » (Figure 2).² Cela provoque une réflexion supplémentaire, ce qui modifie la parité, ou l'orientation de l'image.

Figure 2 : Un symbole "V" est ajouté à la vue 2D de l’arête réfringente couverte de ce prisme Amici pour le différencier des autres surfaces

Distance réduite

La lumière qui traverse une lame plane et parallèle subit un décalage d'image dû à la diffraction (Figure 3). Ce décalage de l'image est fonction de l'épaisseur de la lame (t) et de son indice de réfraction (n).

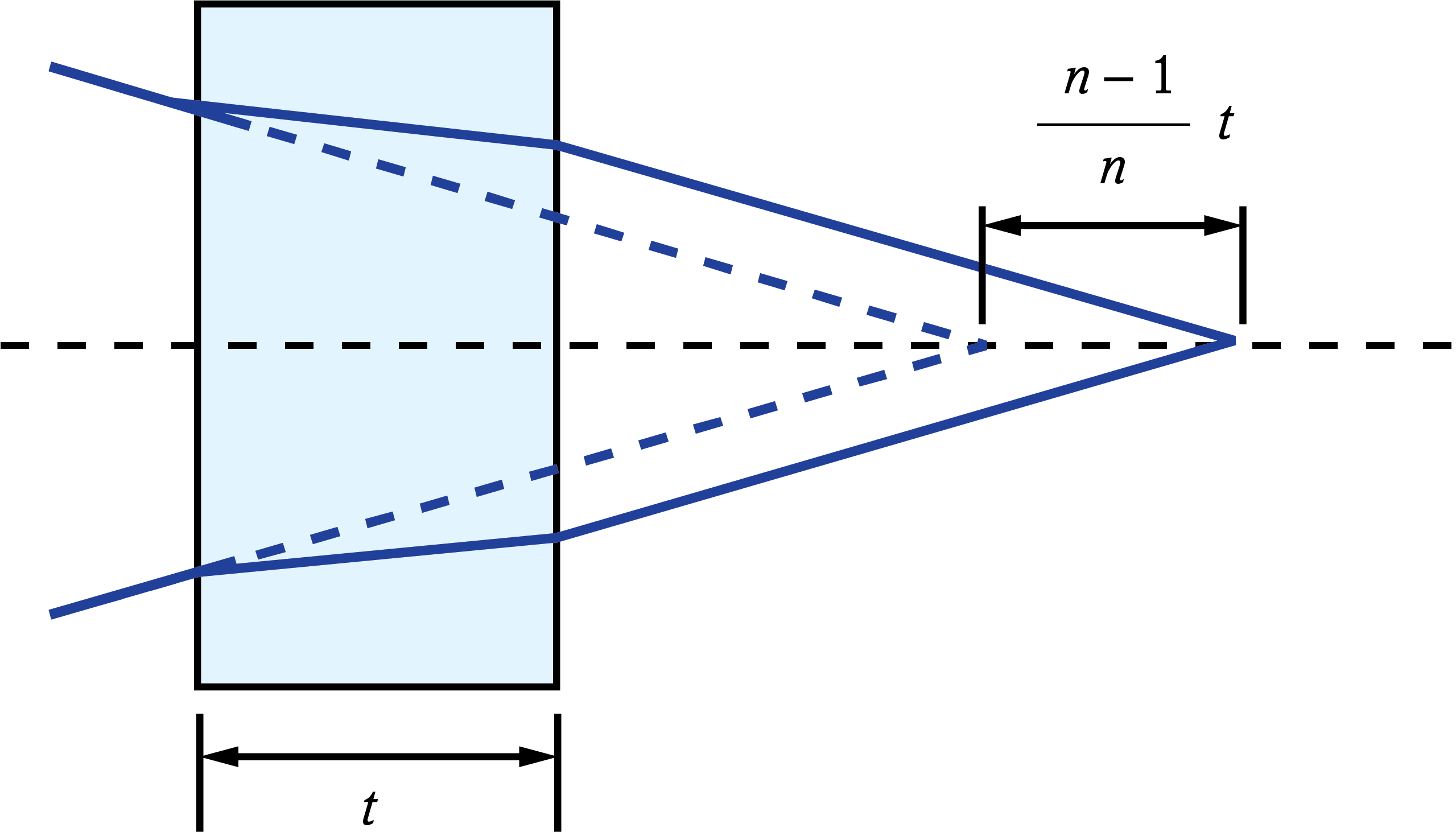
Figure 3 : Décalage de l'image causé par une lame plane et parallèle

Le décalage de l'image à travers le verre peut être compensé en remplaçant la longueur réelle de la trajectoire par la distance réduite. La longueur réelle de la trajectoire dans le verre (L) est divisée par n pour obtenir la distance réduite.² C'est ce que l'on fait souvent dans les diagrammes de tunnel de prismes pour déterminer la longueur de la trajectoire équivalente dans l'espace aérien à travers le prisme (Figure 3).

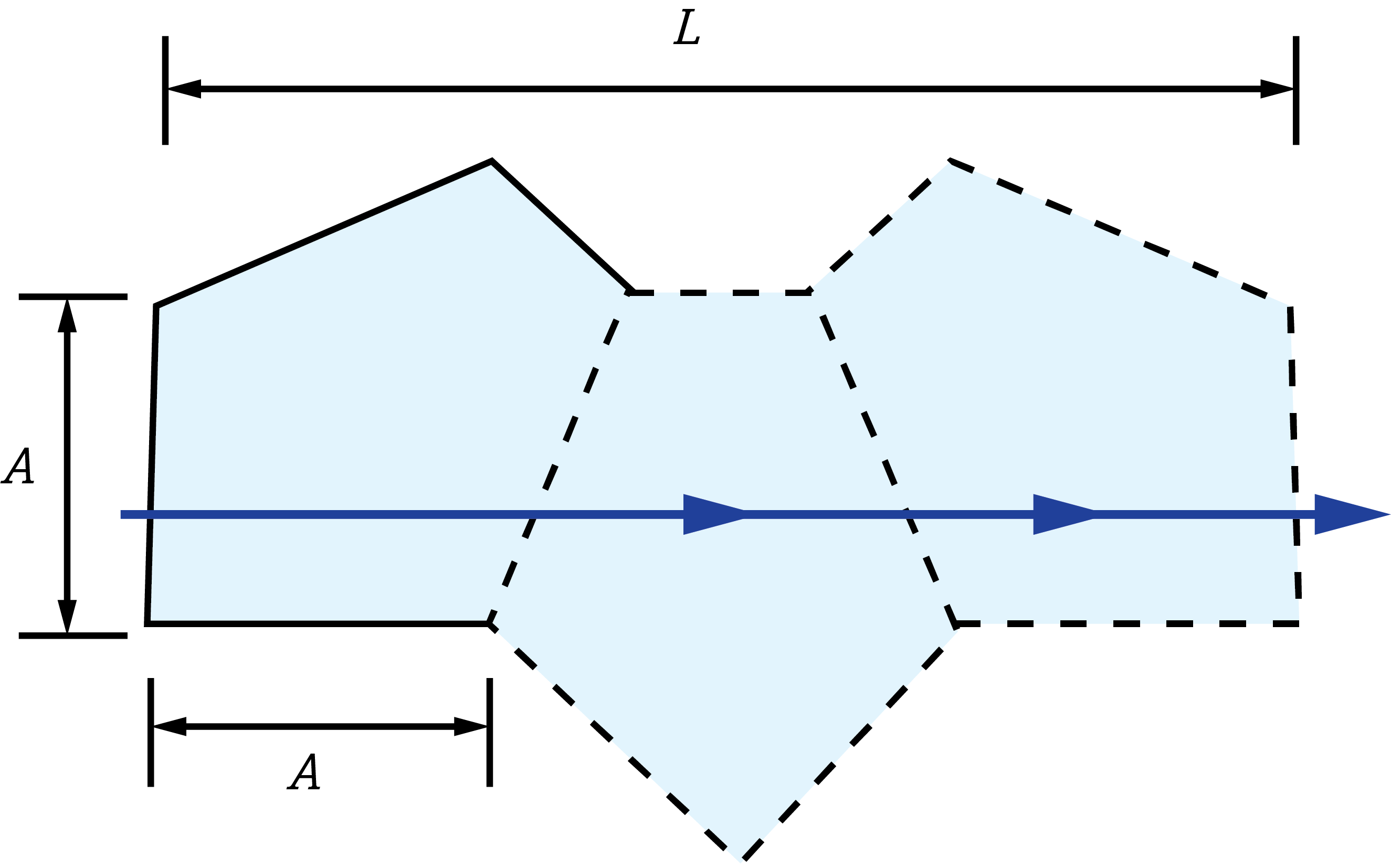
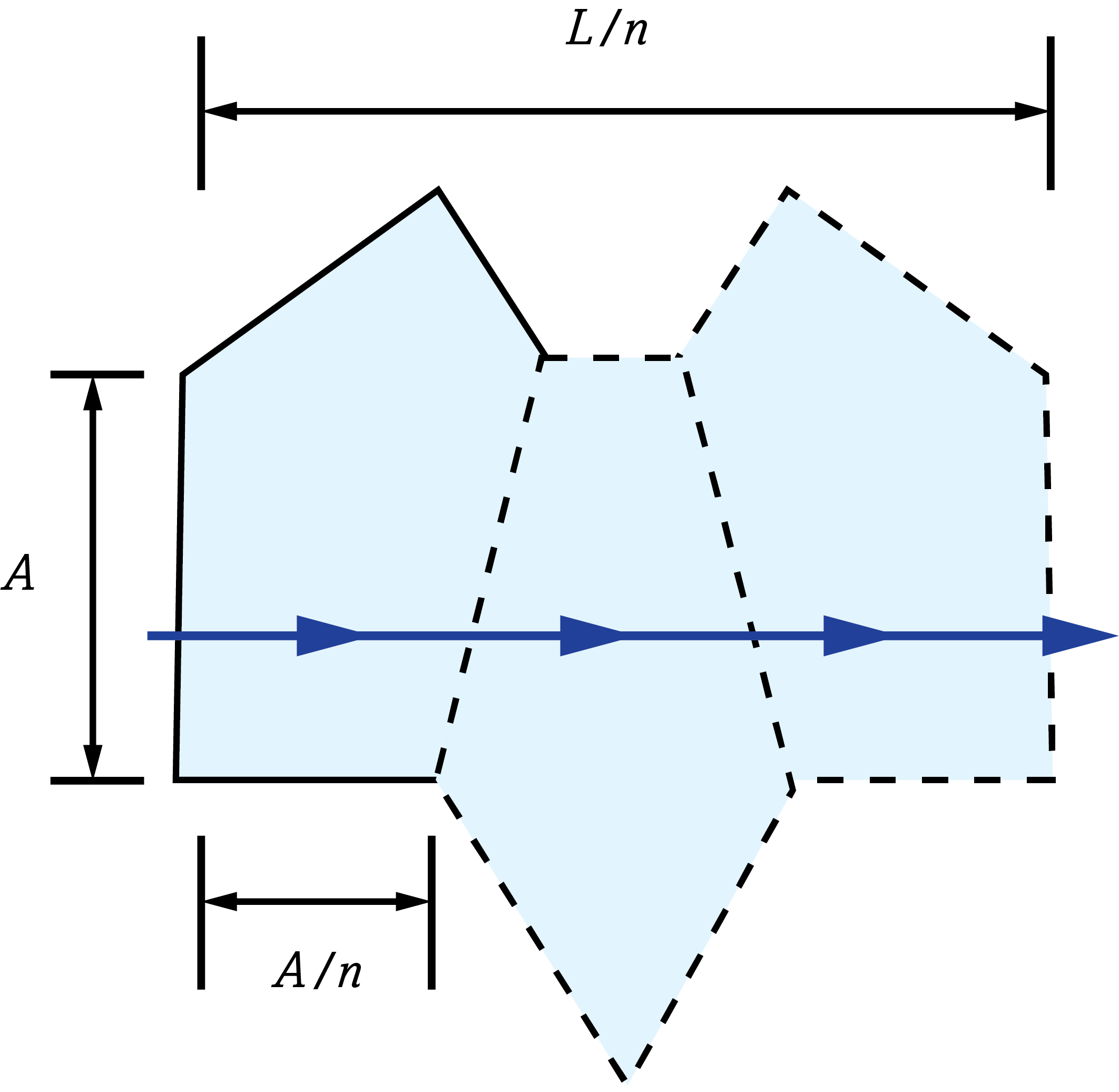
Figure 4 : Diagramme de tunnel à distance réduite d'un prisme penta

Diagrammes de tunnels pour les types de prisme courants

Vous trouverez ci-dessous une collection de diagrammes de tunnel dépliés pour les types de prisme les plus courants. La longueur du chemin optique donnée est la distance réelle parcourue par la lumière dans le prisme, et non la distance réduite. Pour déterminer la distance réduite, divisez la longueur du chemin optique par l'indice de réfraction du prisme.

Prismes à Angle Droit :

Déviation des rayons de 90° ou 180° Produisent des images orientées à gauche en raison d'une seule réflexion Utilisés en combinaison pour le déplacement d’image/de faisceau Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ A $$
			$$ A $$

Prismes de Dispersion Littrow :

Déviation de rayon de 60° en cas de revêtement Produisent des images orientées à droite Disperseront la lumière dans ses composantes spectrales sans reflets lorsqu'ils ne sont pas revêtus Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ A \sqrt{3} $$ $$ \approx 1,7321 A $$

Prismes Penta :

Déviation des rayons de 90° Produisent des images orientées à gauche en raison d'une seule réflexion Un léger décalage du prisme n'affecte pas l'angle droit réel auquel les rayons sont réfléchis Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ A \left( 2 + \sqrt{2} \right)$$ $$ \approx 3,4142 A $$

Prismes en Toit Amici :

Déviation des rayons de 90° Produisent des images orientées à droite L’arête réfringente provoque une réflexion supplémentaire Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ \left( 1 + \frac{\sqrt{2}}{2} \right)A $$ $$ \approx 1,7071A $$

Prismes Dove :

Utilisé avec ou sans traitement Lorsqu'il n'est pas traité, l'image orientée à gauche tourne de deux fois l'angle de rotation du prisme Lorsqu'il est traité, l'image orientée à droite est renvoyée vers elle-même Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ \frac{2 n A}{\sqrt{2 n^2 - 1} - 1} $$
			$$ B $$

Demi Penta Prismes :

Dévient la trajectoire du rayon de 45° Image orientée à droite Combinés avec des Prismes Schmidt pour créer des Prismes Pechan Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ \frac{A}{2} \left(   2 +  \sqrt{2}  \right) $$  $$  \approx  1,7071 A  $$

Prismes Schmidt :

Dévient la trajectoire du rayon de 45° Image orientée à droite Combinés avec des Demi Penta Prismes pour créer des Prismes Pechan Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ A \left( 2 + \sqrt{2} \right) $$  $$  \approx 3,4142 A  $$

Prismes Pechan :

Inversent l'image en la faisant pivoter de 180° Image orientée à droite Combinaison d'un prisme de Schmidt et d'un demi penta prisme Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ \left( 2 + \sqrt{2} \right) \left( \frac{ A_{\tiny{\text{Demi-Penta}}}}{2} + A_{\tiny{\text{Schmidt}}}\right) $$ $$ \approx 3.4142 \left(  \frac{A_{\tiny{\text{Demi-Penta}}}}{2} + A_{\tiny{\text{Schmidt}}} \right) $$

Prismes Rhomboïdes :

Déplacement latéral du faisceau Déplacement latéral équivalent à la longueur du prisme N'inversent pas l'image Voir les options de prismes

Diagramme de trajectoire de rayon 3D	Diagramme de trajectoire de rayon 2D	Schéma du tunnel correspondant	Longueur du chemin optique
			$$ 2D $$

Références

1. Greivenkamp, John E. Field Guide to Geometrical Optics. SPIE Optical Engineering Press, 2004.
2. Hopkins, R. E., “Mirror and Prism Systems," dans Military Standardization Handbook: Optical Design, MIL-HDBK 141, U.S. Defense Supply Agency Washington, DC, 1962.
3. Shack, Roland V. “Prisms.” Dans OPTI 421/521 - Introductory Optomechanical Engineering, University of Arizona, 2016.