Comparaison des aberrations optiques

Identifier les aberrations | Exemples d'aberrations

Les aberrations optiques sont des écarts de par rapport à un modèle mathématique parfait. Il est important de noter qu'elles ne sont pas causées par un quelconque défaut physique, optique ou mécanique. Ils peuvent plutôt être causés par la forme de la lentille elle-même, ou par la disposition des éléments optiques dans un système, en raison de la nature ondulatoire de la lumière. Les systèmes optiques sont généralement conçus à l'aide des principes optiques de premier ordre ou paraxiaux afin de calculer la taille et l'emplacement de l'image. L'optique paraxiale ne tient pas compte des aberrations ; elle traite la lumière comme un rayon et omet donc les phénomènes ondulatoires à l'origine des aberrations. Pour une introduction aux aberrations optiques, voir Chromatic and Monochromatic Optical Aberrations.

Après avoir défini les différents groupes et types d'aberrations optiques chromatiques et monochromatiques, la partie difficile consiste à les reconnaître dans un système, soit par analyse informatique, soit par observation dans le monde réel, puis à corriger le système pour réduire les aberrations. En général, les concepteurs optiques introduisent d'abord un système dans un logiciel de conception de systèmes optiques, tel que Zemax® ou Code V®, pour vérifier les performances et les aberrations du système. Il est important de noter qu'après la fabrication d'un composant optique, les aberrations peuvent être reconnues en observant la sortie du système.

Identification optique des aberrations

Déterminer les aberrations présentes dans un système optique n'est pas toujours une tâche facile, même au stade de l'analyse informatique, car il est fréquent que deux aberrations ou plus soient présentes dans un système donné. Les concepteurs optiques utilisent divers outils pour reconnaître les aberrations et tenter de les corriger, notamment des diagrammes de points, des diagrammes en éventail d'ondes et des diagrammes en éventail de rayons générés par ordinateur. Les diagrammes de points illustrent comment un point lumineux unique apparaît après avoir été imagé par le système. Les diagrammes en éventail des ondes sont des tracés du front d'onde par rapport au front d'onde aplati où une onde parfaite serait plate le long de la direction x. Les diagrammes d'éventail de rayons sont des tracés des points de l'éventail de rayons en fonction des coordonnées de la pupille. Le menu suivant illustre des diagrammes représentatifs d'éventail d'ondes et d'éventail de rayons pour les plans tangentiel (vertical, direction y) et sagittal (horizontal, direction z) où $ \small{H = 1} $ pour chacune des aberrations suivantes : inclinaison $ \left( \small{W_{111}} \right) $, défocalisation $ \left( \small{W_{020}} \right) $, sphérique $ \left( \small{W_{040}} \right) $, coma $ \left( \small{W_{131}} \right) $, astigmatisme $ \left( \small{W_{222}} \right) $, courbure de champ $ \left( \small{W_{220}} \right) $, et distorsion $ \left( \small{W_{311}} \right) $. Il suffit de sélectionner l'aberration qui vous intéresse pour voir chaque illustration.

Nom de l'aberration (coefficient de front d'onde) :

Figure 1 : Motif de la tache d’Airy

Reconnaître les aberrations, surtout au stade de la conception, est la première étape pour les corriger. Pourquoi un concepteur optique souhaite-t-il corriger les aberrations ? La réponse est de créer un système qui est limité par la diffraction, ce qui est la meilleure performance possible. Les aberrations des systèmes limités par la diffraction sont contenues dans la taille du spot de la tache d'Airy, ou la taille de la figure de diffraction causée par une ouverture circulaire (Figure 1).

L'équation 1 peut être utilisée pour calculer la taille du spot de la tache d'Airy $ \small{\left( d \right)} $ où $ \small{\lambda} $ est la longueur d'onde utilisée dans le système et f/# est le nombre f du système.

(1)$$ d = 2,44 \cdot \lambda \cdot \left( f/ \# \right) $$

EXEMPLES D'ABERRATIONS OPTIQUES

Une fois le système conçu et fabriqué, les aberrations peuvent être observées en projetant une source ponctuelle, telle qu'un laser, à travers le système pour voir comment le point unique apparaît sur le plan de l'image. De multiples aberrations peuvent être présentes, mais en général, plus l'image ressemble à une tache, moins il y a d'aberrations ; ceci indépendamment de la taille, car la tache pourrait être agrandie par le système. Les sept exemples suivants illustrent le comportement du rayon si l'aberration correspondante était la seule dans le système, les simulations d'images aberrantes à l'aide de mires de test courantes (Figures 2 à 4) et les actions correctives possibles pour minimiser l'aberration.

Les simulations ont été créées dans Code V® et sont exagérées pour mieux illustrer l'aberration induite. Il est important de noter que les seules aberrations abordées sont celles de premier et de troisième ordre, en raison de leur caractère commun, car la correction des aberrations d'ordre supérieur devient très complexe pour une légère amélioration de la qualité de l'image.

Figure 2 : Mire de distorsion à grille à fréquence fixe

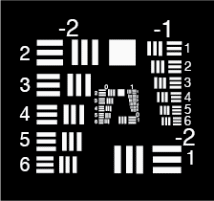
Figure 3 : Mires de résolution de contraste USAF 1951, négatives

Figure 4 : Mire étoilée

Inclinaison – $\small{W_{111}}$
Figure 5a : Représentation de l'aberration d'inclinaison	Figure 5b : Simulation de l'aberration d'inclinaison
Caractérisation Le grossissement de l'image n'est pas correct Causé par l'inclinaison du front d'onde réel par rapport au front d'onde de référence Premier ordre : $ \small{W_{111} = H \cdot \rho \cdot \cos{\left( \theta \right)}} $	Action corrective Modifier le grossissement du système

Défocalisation – $\small{W_{020}}$
Figure 6a : Représentation de l'aberration de défocalisation	Figure 6b : Simulation de l'aberration de défocalisation
Caractérisation Image dans un plan d'image incorrect Causée par une image de référence erronée Utilisée pour corriger d'autres aberrations Premier ordre : $ \small{W_{020} = \rho ^2} $	Action corrective Recentrer le système, trouver une nouvelle image de référence

Sphérique – $\small{W_{040}}$
Figure 7a : Représentation de l'aberration sphérique	Figure 7b : Simulation de l'aberration sphérique
Caractérisation L'image semble floue, les rayons provenant du bord font la mise au point en un point différent de celui des rayons provenant du centre Se produit avec tous les composants optiques sphériques Aberration sur l'axe et hors axe Troisième ordre : $ \small{W_{040} = \rho ^4} $	Action corrective Contrecarrer par défocalisation Utiliser des lentilles asphériques Dédoublement de la lentille Utiliser le facteur de forme de 1 : lentille PCX Indice élevé

Coma – $\small{W_{131}}$
Figure 8a : Représentation de l'aberration de coma	Figure 8b : Simulation de l'aberration de coma
Caractérisation Se produit lorsque le grossissement change par rapport à l'emplacement sur l'image Deux types : Tangentielle (verticale, direction Y) et sagittale (horizontale, direction X) Hors axe uniquement Troisième ordre : $\small{W_{131} = H \cdot \rho ^3 \cdot \cos{\left( \theta \right)}} $	Action corrective Utiliser une lentille doublet espacée avec un diaphragme d’ouverture au centre

Astigmatisme – $\small{W_{222}}$
Figure 9a : Représentation de l'aberration d’astigmatisme	Figure 9b : Simulation de l'aberration d’astigmatisme
Caractérisation Cause deux points de focalisation : L'un dans la direction horizontale (sagittale) et l'autre dans la direction verticale (tangentielle) La pupille de sortie semble elliptique hors de l'axe, le rayon est plus petit dans une direction Hors axe uniquement Troisième ordre : $\small{W_{222} = H^2 \cdot \rho^2 \cos^2{\left( \theta \right)}}$	Action corrective Contrecarrer par défocalisation Utiliser une lentille doublet espacée avec un diaphragme d’ouverture au centre

Courbure de champ – $\small{W_{220}}$
Figure 10a : Représentation de l'aberration de courbure de champ	Figure 10b : Simulation de l'aberration de courbure de champ
Caractérisation L'image est parfaite, mais uniquement sur le plan d'image incurvé Causée par la distribution d'énergie de l'optique Hors axe uniquement Troisième ordre : $\small{W_{220} = H^2 \cdot \rho^2}$	Action corrective Utiliser une lentille doublet espacée

Distorsion – $\small{W_{311}}$
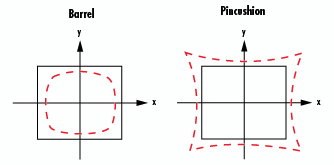Figure 11a : Représentation de l'aberration de distorsion	Figure 11b : Simulation de l'aberration de distorsion en barillet Figure 11c : Simulation de l'aberration de la distorsion en coussinet
Caractérisation Erreur de grossissement quadratique, les points de l'image sont soit trop proches, soit trop éloignés du centre La distorsion positive est appelée distorsion en barillet, la négative est appelée distorsion en coussinet Hors axe uniquement Troisième ordre : $ \small{W_{311} = H^3 \cdot \rho \cdot \cos{\left( \theta \right)}} $	Action corrective Diminuer en plaçant le diaphragme d'ouverture au centre du système

Il est très important de reconnaître les aberrations optiques pour les corriger dans un système optique, car l'objectif est d'obtenir un système limité par la diffraction. Les systèmes optiques et d'imagerie peuvent contenir de multiples combinaisons d'aberrations, qui peuvent être classées comme chromatiques ou monochromatiques. Il est préférable de corriger les aberrations au stade de la conception, où des mesures telles que le déplacement du diaphragme d’ouverture ou la modification du type de lentille optique peuvent réduire considérablement le nombre et la gravité (ou l'ampleur) des aberrations. Dans l'ensemble, les concepteurs optiques s'efforcent de réduire les aberrations de premier et de troisième ordre, principalement parce que la réduction des aberrations d'ordre supérieur ajoute une complexité importante pour une légère amélioration de la qualité de l'image.