Les aberrations optiques chromatiques et monochromatiques
La conception de systèmes optiques n'est jamais une tâche facile ; même les systèmes parfaitement conçus contiennent des aberrations optiques. L'astuce consiste à comprendre et à corriger ces aberrations optiques afin de créer un système optimal. Pour ce faire, il faut considérer les types d'aberrations présentes dans les systèmes optiques.
Les aberrations optiques sont des écarts par rapport à un modèle mathématique parfait. Il est important de noter qu'elles ne sont pas causées par un quelconque défaut physique, optique ou mécanique. Elles peuvent plutôt être causées par la forme de la lentille elle-même, ou par la disposition des éléments optiques dans un système, en raison de la nature ondulatoire de la lumière. Les systèmes optiques sont généralement conçus à l'aide des principes optiques de premier ordre ou paraxiaux afin de calculer la taille et l'emplacement de l'image. L'optique paraxiale ne tient pas compte des aberrations ; elle traite la lumière comme un rayon et omet donc les phénomènes ondulatoires à l'origine des aberrations.
Les aberrations optiques sont nommées et caractérisées de différentes manières. Par souci de simplicité, les aberrations sont divisées en deux groupes : les aberrations chromatiques (présentes lorsque l'on utilise plus d'une longueur d'onde de la lumière) et les aberrations monochromatiques (présentes avec une seule longueur d'onde de la lumière).
ABERRATIONS CHROMATIQUES
Les aberrations chromatiques sont classées en deux catégories : les aberrations transversales et les aberrations longitudinales. L'aberration chromatique longitudinale peut alors être primaire ou secondaire.
L'aberration chromatique transversale (ACT) se produit lorsque la taille de l'image varie en fonction de la longueur d'onde. En d'autres termes, lorsque la lumière blanche est utilisée, les longueurs d'onde rouge, jaune et bleue se concentrent en des points distincts d'un plan vertical (Figure 1). En optique, 656,3 nm (rouge) est appelé lumière C, 587,6 nm (jaune) est appelé lumière d et 486,1 nm (bleu) est appelé lumière F. Ces désignations proviennent des lignes d'émission de l'hydrogène pour les lumières C et F et de l'hélium pour la lumière d.
L'aberration chromatique longitudinale (ACL) se produit lorsque différentes longueurs d'onde se concentrent en différents points le long de l'axe optique horizontal, en raison des propriétés de dispersion du verre. L'indice de réfraction d'un verre dépend de la longueur d'onde, il a donc un effet légèrement différent sur l'endroit où chaque longueur d'onde de la lumière se concentre, ce qui se traduit par des points focaux distincts pour la lumière F, d et C le long d'un plan horizontal.

Figure 1 : Aberration chromatique transversale d'une lentille positive singulet

Figure 2 : Aberration chromatique longitudinale d'une lentille positive singulet

Figure 3 : Lentille achromatique doublet corrigeant l'aberration chromatique longitudinale primaire
La correction primaire de l'ACL est généralement réalisée à l'aide d'une lentille achromatique doublet, composée d'éléments de lentilles positives et négatives d'indices de réfraction différents (Figure 3). Ce type de correction oblige les lumières F et C à se concentrer au même endroit, mais n'a que peu d'effet sur l'emplacement de la lumière d, ce qui laisse une aberration chromatique résiduelle.
Pour corriger cette ACL résiduelle, il faut utiliser une lentille ou un système de lentilles plus complexe pour déplacer le point focal de la lumière d afin qu'il se trouve au même endroit axial que les points focaux F et C. Ce type de correction est généralement obtenu en utilisant une lentille apochromatique, qui est corrigée de manière à ce que trois longueurs d'onde se concentrent au même point, ou une lentille superachromatique, qui est corrigée de manière à ce que quatre longueurs d'onde se concentrent au même point. Les figures 4a à 4d montrent une comparaison du décalage de la mise au point entre les types de systèmes de lentilles susmentionnés.

Figure 4a : Décalage de la mise au point en l’absence de correction de l'aberration avec une lentille singulet

Figure 4b : Décalage de la mise au point avec correction de l'aberration chromatique longitudinale primaire avec une lentille achromatique
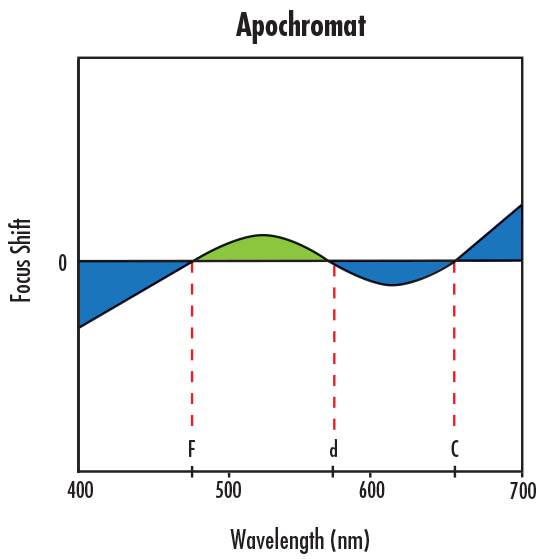
Figure 4c : Décalage de la mise au point avec correction de l'aberration chromatique longitudinale secondaire avec un objectif apochromatique

Figure 4d : Décalage de la mise au point avec correction de l'aberration chromatique longitudinale secondaire avec un objectif superachromatique
ABERRATIONS MONOCHROMATIQUES
Les types d'aberrations monochromatiques sont beaucoup plus nombreux que les aberrations chromatiques. C'est pourquoi ils sont étiquetés avec des coefficients de front d'onde en plus des noms. Par exemple, l'aberration sphérique a un coefficient de front d'onde de $ \small{W_{040}} $. Ce coefficient de front d'onde résulte de la sommation mathématique qui donne la différence réelle entre le front d'onde parfait et le front d'onde aberré :
Dans l'équation 1, $ \small{W_{klm}} $ est le coefficient du front d'onde, $ \small{\text{H}} $ est la hauteur normalisée de l'image, $ \small{\rho} $ est l'emplacement dans la pupille, et $ \small{\theta} $ est l'angle entre les deux, qui résulte du produit de points des deux vecteurs. Une fois le coefficient du front d'onde connu, le numéro d'ordre peut être déterminé en additionnant l et $ \small{k} $. Cependant, cela créera toujours un nombre pair. Les aberrations optiques étant souvent désignées par les termes premier, troisième, cinquième ordre, etc., si $\small{k + 1 = 2} $, il s'agit d'une aberration de premier ordre, si $\small{k + 1 = 4} $, il s'agit d'une aberration de troisième ordre, etc. En général, seules les aberrations de premier et de troisième ordre sont nécessaires pour l'analyse du système. Les aberrations d'ordre supérieur existent mais ne sont pas couramment corrigées dans les systèmes optiques en raison de la complication qu'elles ajoutent au système. En général, la complexité de la correction des aberrations d'ordre supérieur ne vaut pas l'amélioration de la qualité de l'image. Les aberrations monochromatiques courantes du troisième ordre et leurs équations et coefficients correspondants sont énumérés dans le tableau 1.
| Nom de l'aberration | Coefficient de front d'onde | Équation |
|---|---|---|
| Inclinaison | $$ W_{111} $$ | $$ W_{111} \cdot H \cdot \rho \cdot \cos{\left( \theta \right)} $$ |
| Défocalisation | $$ W_{020} $$ | $$ W_{020} \cdot \rho ^2 $$ |
| Sphérique | $$ W_{040} $$ | $$ W_{040} \cdot \rho ^4 $$ |
| Coma | $$ W_{131} $$ | $$ W_{131} \cdot H \cdot \rho ^3 \cdot \cos{\left( \theta \right)} $$ |
| Astigmatisme | $$ W_{222} $$ | $$ W_{222} \cdot H^2 \cdot \rho^2 \cdot \cos^2{\left( \theta \right)} $$ |
| Courbure de champ | $$ W_{220} $$ | $$ W_{220} \cdot H^2 \cdot \rho^2 $$ |
| Distorsion | $$ W_{311} $$ | $$ W_{311} \cdot H^3 \cdot \rho \cdot \cos{\left( \theta \right)} $$ |
Tableau 1 : Aberrations optiques courantes du troisième ordre
Les systèmes optiques et d'imagerie peuvent contenir de multiples combinaisons d'aberrations optiques. Ces aberrations optiques peuvent être classées en aberrations chromatiques ou monochromatiques. Les aberrations dégraderont toujours la qualité de l'image, et une très grande partie de la conception optique est axée sur la reconnaissance et la réduction de ces aberrations. La première étape de la correction des aberrations consiste à comprendre les différents types d'aberrations et la manière dont elles affectent les performances du système. Grâce à ces connaissances, il est possible de concevoir le meilleur système possible. Pour des informations détaillées sur l'identification et la correction des aberrations chromatiques et monochromatiques, voir Comparaison des aberrations optiques.
Référence
- Dereniak, Eustace L., and Teresa D. Dereniak. Geometrical and Trigonometric Optics. Cambridge : Cambridge University Press, 2008.














ou consulter les numéros d’autres pays
facile à utiliser
entrer les numéros de stock pour commencer
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
L'entreprise Edmund Optics GmbH en Allemagne agit comme un mandataire d'Edmund Optics Ltd au Royaume-Uni. Le titulaire du contrat est Edmund Optics Ltd au Royaume-Uni.