Les défis de spécifier le LIDT pour les lasers CW

Les circonstances d'utilisation affectent davantage le seuil de dommage des lasers à onde continue (CW) que celui des systèmes à laser pulsé, de sorte que les utilisateurs de systèmes à laser CW doivent faire preuve de plus de prudence. Le seuil de dommage des lasers CW est normalement spécifié comme une densité de puissance linéaire mesurée à une longueur d'onde donnée. Les utilisateurs ne doivent pas trop se fier au seuil de dommage CW spécifié d'un composant optique sans tenir compte des nombreux paramètres qui peuvent modifier la valeur : puissance du laser, diamètre du faisceau et conditions de test ambiantes, entre autres.

Définitions & Différences :

La norme ISO définit le seuil de dommage induit par le laser (LIDT) comme « la plus grande quantité de rayonnement laser incidente sur le composant optique pour laquelle la probabilité extrapolée de dommage est nulle ».¹ Les lasers pulsés et CW diffèrent dans leur mode de fonctionnement et, par conséquent, présentent des mécanismes de dommage différents. Le LIDT pulsé est déterminé par des tests à un ou plusieurs tirs, tandis que le LIDT CW est testé en exposant une optique à la fluence constante du laser pendant un certain temps. Les dommages causés par les lasers pulsés, mesurés par un temps d'exposition de l'ordre de nanosecondes à femtosecondes, résultent généralement du champ électrique ou d'une contrainte mécanique. (Pour plus d’informations, consultez le Tableau 1 de notre Note d'application : Comprendre et spécifier le LIDT des composants laser). Les durées d'impulsion supérieures à 100 picosecondes entraînent souvent une fusion conventionnelle. Les dommages causés par le laser CW sont dus à un échauffement ou à une défaillance mécanique due à une contrainte thermique dans l'optique. Par conséquent, les dommages des lasers quasi-CW, où le temps d'exposition est de l'ordre de microsecondes, sont causés par une combinaison de champ électrique et de dommages thermiques.

Les défis particuliers de spécifier et tester la LIDT CW

Les tests des seuils de dommage avec les lasers à onde continue posent des problèmes qui ne se posent pas dans les tests de dommage avec les lasers pulsés. Parmi les principaux paramètres à prendre en compte pour les tests CW, citons le temps d'exposition, le diamètre du faisceau, le matériau de construction, les défauts sur l'échantillon et le choix du montage. Les conditions ambiantes doivent également être prises en considération, en particulier tout flux d'air au-dessus de l'optique.

Le temps d'exposition est l'intervalle pendant lequel l'optique en question est soumise à la puissance du laser. Les temps d'exposition pour les tests de dommages causés par le laser CW sont supérieurs à une seconde mais généralement de cinq secondes à une minute par site de test, ou jusqu'à ce que l'échantillon échoue.² Une autre considération liée au temps d'exposition est le temps de repos entre chaque test. Si l'échantillon ne dispose pas d'un temps suffisant pour se « détendre » thermiquement, l'exposition suivante sera plus difficile sur l'échantillon que la précédente. Ceci est quelque peu lié à la fréquence de répétition des lasers pulsés, mais sur une échelle de temps plus longue. Cela donne plus d'incertitude dans le monde réel ; combien de temps l'utilisateur donnera-t-il à l'optique pour se rétablir ? Ce temps de repos peut littéralement faire ou défaire l'optique.

Le nombre de défauts avec lesquels le faisceau interagira sera déterminé par le diamètre du faisceau choisi pour le test. Il est important de comprendre toute imperfection sur ou sous la surface de l'optique. Les défauts peuvent être des dommages sous la surface comme des fissures ou des rainures, ou bien des imperfections de la surface comme des défauts du traitement ou des contaminants sur l'optique. Les dommages causés au traitement résultent généralement d'une absorption facilitée par la poussière ou les rayures à la surface. Une absorption d'énergie suffisante à la surface peut provoquer la délamination du traitement.² En principe, plus le faisceau rencontre de défauts, plus le seuil de dommage sera bas.

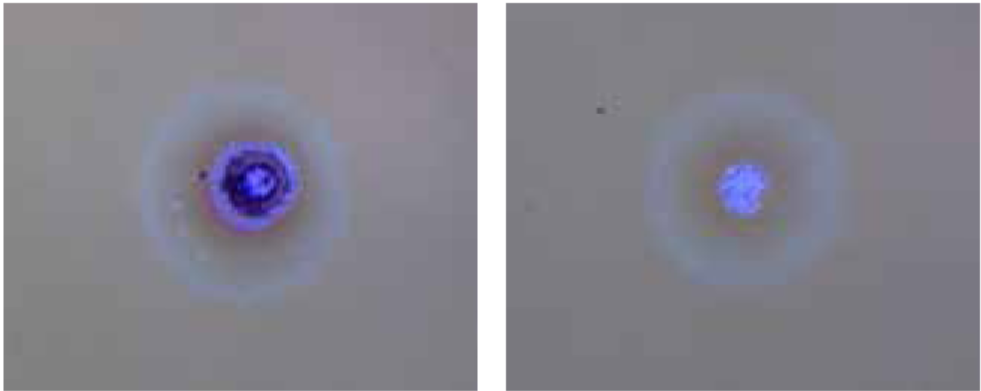
Figure 1 : Différentes morphologies de dommages laser résultant de différentes causes.

La conductivité thermique et l'absorption du matériau du substrat déterminent le profil dans lequel la chaleur est distribuée dans toute l'optique. Par exemple, les optiques à transmission en silicium et en germanium laissent passer la lumière infrarouge (IR) mais pas la lumière visible, ce qui entraîne une absorption sur la première surface. ³ Cette première absorption de surface entraîne ensuite une augmentation de la température à la surface de l'optique qui, à son tour, provoque un gradient de température important. La dimension du gradient de température peut déterminer s'il y aura ou non des dommages à l'échantillon. Par conséquent, les optiques avec des traitements hautement réfléchissants sont souvent utilisées lors des tests de lasers CW en raison de leur capacité à réfléchir une partie de la chaleur vers des régions éloignées de l'optique.

La manière dont l'échantillon est monté est un autre paramètre important à prendre en compte. Parfois, une contrainte mécanique peut être introduite par la monture, ce qui peut augmenter les effets de la contrainte thermique due à l'absorption du laser. Le fait que l'échantillon soit monté ou non avec de la colle a également une incidence sur la façon dont la chaleur est transférée dans l'optique. En outre, le choix du montage introduit la possibilité d'un refroidissement par convection en raison du flux d'air sur l'échantillon. La présence d'un dissipateur thermique et l'efficacité avec laquelle il absorbe le rayonnement provenant de l'optique peuvent considérablement augmenter le seuil de dommage de l'échantillon.

Mise à l'échelle du seuil de dommage des lasers CW :

Une étude menée par Slinker, et al. (2019), établit une corrélation entre les dommages induits par le laser en ondes continues et l'augmentation de température de la surface optique au centre du faisceau due à l'absorption. Pour les systèmes laser quasi-CW et CW, l'équation de diffusion de la chaleur est capable de prédire et de mettre à l'échelle le LIDT. Deux cas sont pris en compte lors de la modélisation du seuil de dommage des optiques hautement réfléchissantes : l'éclairage par inondation et l'éclairage ponctuel.⁴

Un éclairage par inondation est considéré comme une grande zone d'éclairage d'une optique fine et réfléchissante avec un détecteur monté sur un dissipateur thermique. L'éclairage ponctuel est une petite zone d'éclairage par rapport à l'épaisseur d'une optique réfléchissante autonome.⁴

Si la convection et le rayonnement sont ignorés à chaque surface, l'augmentation de température sur la surface au centre du faisceau, au fil du temps $ \left( \small{t} \right) $, peut être déterminée par :⁴

(1)$$ T \! \left( \phi, t \right) = T_0 + \frac{\alpha \phi}{k} + \left[ \frac{1 - \exp{\left( - \frac{t'}{t} \right)}}{\sqrt{\pi}} \sqrt{\frac{t}{t'}} + \text{erfc} \, {\left( \sqrt{\frac{t'}{t}} \right)} \right]$$

(1)

$$ T \! \left( \phi, t \right) = T_0 + \frac{\alpha \phi}{k} + \Big[ A + B \Big]$$

(1.1)

$$ A_1 = \frac{1 - \exp{\left( - \frac{t'}{t} \right)}}{\sqrt{\pi}} \sqrt{\frac{t}{t'}} $$

(1.2)

$$ B_1 = \text{erfc} \, {\left( \sqrt{\frac{t'}{t}} \right)} $$

Temps caractéristique :

(2)$$ t' = \frac{r^2}{4k}c_p \rho $$

(2)

$$ t' = \frac{r^2}{4k}c_p \rho $$

Où $ \small{T_0} $ est la température initiale de l'échantillon, $ \small{\alpha} $ est l'absorption fractionnaire à la longueur d'onde d'irradiation, $ \small{\phi} $ est la densité de puissance linéaire, $ \small{k} $ est la conductivité thermique du substrat, $ \small{\rho} $ est la densité de l'échantillon, $ \small{r} $ est le rayon de l'échantillon et $ \small{c_p} $ est la capacité thermique spécifique $\left[ \tfrac{\text{J}}{\text{g K}} \right] $.

Le seuil de dommage nous indique la probabilité que l'optique soit défaillante sous une certaine quantité de rayonnement laser. Pour les lasers CW, ce seuil peut être considéré comme une densité de puissance linéaire, $ \small{\phi_{DT}} \left[ \tfrac{\text{W}}{\text{cm}} \right] $, dont il a été prouvé qu'elle diminue avec l'augmentation du temps d'exposition. Lorsque les considérations environnementales sont ignorées, la valeur minimale de la densité de puissance linéaire en fonction du temps d'exposition peut être résolue en réglant $ \small{T} $ sur une défaillance ou une température critique $ \small{T_c} $, et en résolvant pour $ \small{\phi} $ :⁴

(3)$$ \phi_{DT} = \frac{k \left( T_c - T_0 \right)}{\alpha} $$

(3)

$$ \phi_{DT} = \frac{k \left( T_c - T_0 \right)}{\alpha} $$

Dans ces conditions, la puissance laser nécessaire pour endommager l'échantillon est une densité de puissance linéaire constante. En outre, la norme ISO prescrit une mise à l'échelle en fonction de la densité de puissance linéaire plutôt qu'en fonction de l'irradiance.⁴
Alternativement, en prenant en considération les conditions d'essai ambiantes, pour une optique réfléchissante autonome, l'augmentation de température sur la surface au cours du temps $\left( \small{t} \right)$ est :⁴

(4)$$ T \! \left( I, t \right) = T_{\small{\text{Air}}} + \frac{\alpha I}{2 h_{\small{\text{eff}}}} + \left( T_0 - T_{\small{\text{Air}}} - \frac{\alpha I}{2 h_{\small{\text{eff}}}} \right) \exp{\left( - \frac{t}{t'}\right)} $$

(4)

$$ T \! \left( I, t \right) = T_{\small{\text{Air}}} + \frac{\alpha I}{2 h_{\small{\text{eff}}}} + A_2 $$

(4.1)

$$ A_2 = \left( T_0 - T_{\small{\text{Air}}} - \frac{\alpha I}{2 h_{\small{\text{eff}}}} \right) \exp{\left( - \frac{t}{t'} \right)} $$

Temps caractéristique :

(5)$$ t' = \frac{L}{2 h_{\small{\text{eff}}}} c_p \rho $$

(5)

$$ t' = \frac{L}{2 h_{\small{\text{eff}}}} c_p \rho $$

Où $ \small{T_0} $ est la température initiale de l'échantillon, $ \small{T_{\text{Air}}} $ est la température de l'air entourant l'échantillon, $ \small{L} $ est l'épaisseur de l'échantillon, $ \small{I} $ est l'irradiance $ \left[ \tfrac{\text{W}}{\text{cm} ^2} \right] $, $ \small{\alpha} $ est l'absorbance fractionnaire à la longueur d'onde d'irradiation, et $ \small{t} $ est le temps d'exposition. Dans les deux équations ci-dessus, $ \small{h_{\text{eff}}}$ est le coefficient de convection effectif - la somme des contributions de la convection et de l'irradiation. Ce coefficient est doublé pour tenir compte des deux surfaces de l'échantillon.

Toujours en gardant à l'esprit les conditions ambiantes, lorsqu'il y a un flux d'air important au-dessus de l'optique et un rayonnement provenant de la surface de l'optique, l'irradiance du seuil de dommage peut être calculé par :⁴

(6)$$ I_{DT} \! \left( t \right) = \frac{2 h_{\small{\text{eff}}} \left( T_c - T_{\small{\text{Air}}} \right)}{\alpha \left[ 1 - \exp{\left( -\tfrac{t}{t'} \right)} \right]} $$

(6)

$$ I_{DT} \! \left( t \right) = \frac{2 h_{\small{\text{eff}}} \left( T_c - T_{\small{\text{Air}}} \right)}{\alpha \left[ 1 - \exp{\left( -\tfrac{t}{t'} \right)} \right]} $$

Ce seuil de dommage de l'irradiation diminue jusqu'à une valeur minimale :⁴

(7)$$ I_{DT} = \frac{2 h_{\small{\text{eff}}} \left(T_c - T_{\small{\text{Air}}} \right)}{\alpha} $$

(7)

$$ I_{DT} = \frac{2 h_{\small{\text{eff}}} \left(T_c - T_{\small{\text{Air}}} \right)}{\alpha} $$

Figure 2 : L'irradiation est mise à l'échelle en fonction du temps d'exposition, dans deux conditions d'essai - montrant finalement l'effet du flux d'air sur l'échantillon pendant l'essai.⁴

Figure 3 : Le seuil de dommage des échantillons exposés aux lasers quasi-CW et CW diminue à mesure que le diamètre du faisceau et le temps d'exposition augmentent.

Conclusion

Pour tous les diamètres de faisceau considérés, le seuil de dommage des échantillons exposés aux lasers quasi-CW et CW diminue avec l'augmentation du diamètre du faisceau et du temps d'exposition. Plus le faisceau est grand, plus il est probable qu’il rencontre de multiples défauts sur l'optique, ce qui abaisse le seuil de dommage. La façon dont la chaleur se disperse à travers l'échantillon dépend des dimensions et de la capacité thermique du substrat utilisé. Dans des conditions où il y a un flux d'air à grande vitesse sur l'échantillon, la température à la surface de l'optique est fortement réduite et donc, le seuil de dommage est beaucoup plus élevé qu'une optique non refroidie.

La partie la plus difficile de la spécification du LIDT pour les systèmes laser CW consiste à tester les échantillons dans des conditions reproductibles. Les diverses applications nécessitent des puissances laser, des diamètres de faisceau et d'autres paramètres utiles différents, et certains utilisateurs ne seront pas en mesure de recréer l'environnement dans lequel l'optique a été testée. Le montage, le temps de repos, les conditions ambiantes et plusieurs autres paramètres peuvent modifier le seuil de dommage d'une optique. La variété des conditions de test mentionnées dans cette note d'application est à l'origine des défis que représente la spécification du LIDT pour les lasers CW.

Références

Lasers and laser-related equipment — Test methods for laser-induced damage threshold — Part 1: Definitions and general principles. (n.d.). Retrieved December 14, 2020, from https://www.iso.org/obp/ui/
Palmer, J. R. (1983). Continuous Wave Laser Damage on Optical Components. Optical Engineering, 22(4), 435-446.
Palmer, J. R. (1989). Thermal Shock: Catastrophic Damage To Transmissive Optical Components In High Power Continuous Wave And Repetitive Pulsed Laser Environment. Proceedings of SPIE, 1047, 87-140.
Slinker, K., Pitz, J., Sihn, S., & Vernon, J. P. (2019). Determining and scaling continuous-wave, laser-induced damage thresholds of thin reflectors. Optics Express, 27(4), 4748-4757.

More Resources

Ce contenu vous a-t-il été utile ?

Merci d'avoir évalué ce contenu !