Le choix d’un objectif d’imagerie - considérations plus poussées

Cette note correspond à la Section 6.3 du Guide de Ressources en Imagerie.

Section précédente Section suivante

La section précédente a expliqué la sélection des objectifs principalement du point de vue de l'objectif en tant que composant final à choisir dans le système de vision industrielle. Cette section aborde le choix de l'objectif et de la caméra de manière holistique, en choisissant les deux en même temps, en fonction de ce qui est important pour l'application spécifique. Cette section présente un exemple partant de zéro où un code-barres 2D doit être imagé à une distance de 200 mm, comme le montre la Figure 1.

Figure 1 : Image du code-barres 2D qui doit être imagé à une distance de 200 mm.

La première étape du choix d'un objectif consiste à considérer l'objet à inspecter et à le décomposer en ses éléments constitutifs. Quelles sont les caractéristiques importantes ? Quelle est la taille de ces caractéristiques ? De combien de pixels ai-je besoin pour couvrir la caractéristique que j'essaie d'observer afin que mon logiciel de vision industrielle fonctionne correctement ?

Souvent, le meilleur point de départ est la taille des caractéristiques et la couverture de pixels. Pour le code-barres de la Figure 1, ces chiffres sont assez simples. La taille des caractéristiques est de 100 µm, avec un espace vide d'au moins 100 µm entre les caractéristiques. Cela signifie que la fréquence à laquelle correspond cette caractéristique est de 5$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ (voir Résolution pour un rappel de cette équation) dans l'espace objet. Ce chiffre est la première pièce du puzzle pour déterminer le grossissement nécessaire de l'objectif.

Ensuite, il faut prendre en compte l'ensemble du champ de vision (FOV). Il s'agit non seulement de la taille du code-barres lui-même, mais aussi de l'espace disponible pour l'incertitude de la position dans le champ visuel. Si le code-barres mesure 25 mm x 25 mm, on peut dire qu'un FOV de 35 mm est nécessaire. Dans cet exemple particulier, il est nécessaire d'avoir au moins trois pixels couvrant chaque caractéristique du code-barres. La taille de l'élément sur le code-barres étant de 100 µm, il est donc nécessaire d'avoir au moins 33 µm par pixel sur le plan de l'objet.

À ce stade, différentes caméras peuvent être évaluées pour voir s'il est possible d'y parvenir. Afin de limiter les coûts, il peut être important de commencer par une résolution aussi petite que possible. Dans le monde actuel de la vision industrielle, il s'agit souvent d'une résolution de 0,3 Mpx, ou VGA (640x480). Si l'on regarde le rapport d'aspect du capteur, il est exactement de 4:3. Toutefois, le champ de vision nécessaire est de 1:1 ; cela signifie que la petite dimension du capteur (480 pixels) devra être utilisée pour correspondre au champ de vision de 35 mm, et que la grande dimension le dépassera et qu'il y aura probablement quelques pixels gaspillés.

Comme 480 pixels vont être répartis sur 35 mm d'espace, chaque pixel correspond à 110 µm dans l'espace objet. Cette caméra est certainement insuffisante pour cette application, et il est nécessaire d'avoir une résolution environ 3 fois meilleure. En refaisant les calculs avec un capteur 1600x1200 et des pixels de 4,5 µm, chaque pixel occupe maintenant 29 µm, ce qui est suffisant. Mais comment cela correspond-il à l'espace image avec une caméra et un objectif ? A ce stade, le système doit être relié au grossissement.

Comme ce capteur 1600 x 1200 possède des pixels dont la taille correspond à 4,5 µm, les dimensions sont de 7,2 mm x 5,4 mm. En utilisant l' équation 4 de la section Basic Lens Selection, le grossissement requis est de 0,15X. Il est maintenant possible d'utiliser ce grossissement pour déterminer quel objectif est nécessaire, ainsi que ce que le système d'imagerie doit être en mesure d'atteindre du point de vue de la résolution afin d'imager correctement le code-barres. Puisqu'un capteur a été choisi, l'équation 3 de Basic Lens Selection peut maintenant être utilisée pour déterminer la distance focale de l'objectif. En utilisant l'équation 3, la distance focale requise sur la base de la distance de travail (WD) de 200 mm est de 30 mm. Cependant, le grossissement requis (0,15X) peut être obtenu avec un objectif de 25 mm à une distance de 230 mm ; dans cet exemple, cela suffit. Un objectif préliminaire a maintenant été choisi, mais peut-il fonctionner en fonction de la résolution requise ?

La résolution requise dans l'espace objet est de 5$ \small{ \tfrac{\text{lp}}{\text{mm}}} $. Si l'on convertit ce chiffre en espace image en le divisant par le grossissement, 33$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ sont nécessaires pour voir l'objet correctement. Ce nombre doit être comparé à deux chiffres : la fréquence de Nyquist du capteur et la fonction de transfert de modulation (FTM) de l'objectif utilisé. Voir Résolution pour plus d'informations sur la fréquence de Nyquist. L'équation 1 décrit la fréquence de Nyquist d'un capteur comme suit :

Où s est la taille du pixel. En utilisant l' équation 1, un capteur avec des pixels de 4,5 µm a une fréquence de Nyquist de 111$ \small{ \tfrac{\text{lp}}{\text{mm}}} $. Étant donné que cette valeur est supérieure aux 33$ \small{ \tfrac{\text{lp}}{\text{mm}}} $, cette caméra est une bonne choix. Le lecteur attentif pourra noter que cela renvoie au fait que trois pixels couvrent notre caractéristique et que nous sommes, sans surprise, à environ 3X en dessous de la fréquence de Nyquist. Ces calculs ont été inclus ici par souci d'exhaustivité.

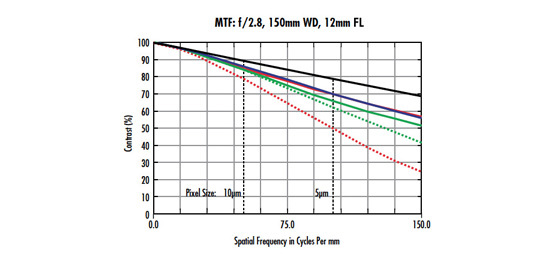
La courbe FTM (MTF en anglais) d'un objectif à focale fixe de 25 mm de la série C à partir d'une distance focale de 166 mm est présentée à la Figure 2 (pour plus d'informations sur la lecture d'une courbe FTM, voir la section Fonction de transfert de modulation). En observant la courbe, on constate que l'objectif de 25 mm atteint environ 83% de contraste à 33$ \small{ \tfrac{\text{lp}}{\text{mm}}} $, ce qui est plus que suffisant pour bien l'imager.

Figure 2 : Courbe FTM d'un objectif à distance focale fixe de la série C de 25 mm qui atteint une résolution plus que suffisante pour cet exemple.

En règle générale, la valeur de contraste minimale requise pour qu'un objectif d'imagerie puisse résoudre correctement un objet est de 20%, ce qui signifie que cet objectif a une résolution plus que suffisante pour voir ce code-barres de manière satisfaisante.

Ceci n’est qu’un des facteurs lors du choix d'un objectif pour une application donnée. La FTM est affectée par plusieurs facteurs (expliqués en détail dans Courbes FTM et performances des objectifs), et souvent, elle n'est pas simple. Les paragraphes suivants expliquent en détail comment examiner spécifiquement un objectif et comment il s'adapte à une caméra.

L'évolution des performances d'un objectif

Les fournisseurs d’objectifs sont en mesure de fournir des courbes FTM sur mesure en fonction de l'utilisation de l’objectif. Dans l'exemple du code-barres ci-dessus, la FTM de l'objectif de 25 mm a été référencée pour déterminer si la reproduction du contraste était suffisante pour le code-barres qu'il reproduisait. Nous allons maintenant développer ce point en utilisant un autre exemple, mais avec le même objectif, pour montrer que les choses ne se passent pas toujours comme prévu.

La Figure 3 montre deux courbes FTM différentes du même objectif de distance focale fixe de 25 mm à la même distance de travail (fournissant un grossissement de 0,76X), mais des f/#s et des gammes de longueurs d'onde différents. On ne croit guerre qu’il s’agit du même objectif ! Ce qu'il faut retenir, c'est qu'il ne suffit pas de regarder les courbes FTM sur les fiches techniques pour expliquer de manière adéquate les performances d'un objectif sur l'ensemble de sa gamme, et que des courbes spécifiques sont nécessaires.

Figure 3 : La FTM d'un objectif haute résolution de 25 mm à différents réglages, ce qui souligne l'importance de comparer les courbes spécifiques des objectifs.

En se basant sur la FTM d'un objectif donné, il est possible de déterminer la taille minimale de l'élément résoluble dans l'espace objet. Cependant, les courbes FTM sont toujours dans l'espace image, ce qui signifie que les informations de l'espace image doivent être transformées en informations de l'espace objet. Heureusement, il suffit de mettre à l'échelle en utilisant le grossissement. L'exemple suivant illustre comment effectuer ces calculs sur la base des courbes de la Figure 3 comme point de départ. En supposant un contraste minimum de 20% pour cet exemple, l'objectif du haut peut résoudre 250$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ dans l'espace image, ce qui est déterminé en trouvant la fréquence sur la courbe qui correspond à un contraste de 20%. En utilisant l'équation 2, la taille du pixel (ou dans ce cas, la résolution de l'espace image
$ \small{\xi _{\small{\text{Espace image}}}} $ converti d'une fréquence à un objet physique) est calculée pour être :

La mise à l'échelle par le grossissement (0,076X) donne :

En comparaison, l'objectif avec la courbe en bas de la Figure 3 ne peut imager avec certitude qu'un objet de 282 µm (en utilisant les mêmes calculs que dans l'exemple ci-dessus). L'exemple de la page précédente suppose également que la caméra/le capteur exactes n'ont pas encore été choisis, ce qui fait de l'optique le composant limitatif du système d'imagerie. Si le capteur de la caméra avait été choisi avant l'objectif, ce dernier devrait être capable de résoudre la taille de pixel du capteur utilisé.

En reprenant l'exemple de la page précédente, si l'on avait choisi un appareil photo équipé du capteur Sony IMX250 avec des pixels de 3,45 µm, l'équation 2 permettrait d'obtenir une résolution de l'espace image de 144,9 $ \small{ \tfrac{\text{lp}}{\text{mm}}} $. En regardant la courbe FTM, l'objectif atteint un contraste de >40%, ce qui est plus que suffisant pour la plupart des applications. Cependant, en utilisant le même calcul que dans l'équation 3 pour passer à l'échelle de l'espace objet, des pixels de 3,45 µm ne correspondent qu'à un objet de 45 µm, ce qui signifie que le capteur serait le composant limitant du système, puisque l'objectif est capable d'une résolution de 26 µm dans l'espace objet. Toutes ces considérations doivent être prises en compte lors de la détermination de l'objectif approprié pour une application donnée, afin de trouver la solution optimale à un problème de vision industrielle.

Section précédente Section suivante

Ressources recommandées

 Note d'application

Résolution

 Note d'application

La fonction de transfert de modulation (FTM)